esercitazione n. 6

Laboratorio di Chimica del Restauro e della Conservazione. A.A. 2004/05

M.P. Sammartino, G. Favero, G. Visco

  Non potendo usare per l'esercitazione circa 60-70 monete antiche con le caratteristiche richieste abbiamo deciso di simulare il set seriale con monete coeeve prodotte nel 2002 da 4 paesi europei con le caratteristiche qui di seguito.

  L'esercitazione simula la misura (microinvasiva) di vari parametri utili a classificare monete fuoricorso e/o antiche. I dati facilmente ottenibili sono poi utilizzati per tentarne una descrizione con l'analisi multivariata e chemiometria. Come al solito misurando si scoprira' che anche la cosa piu' semplice e' difficile se si vuole accuratezza, pertinenza e rappresentativita'.

  Vediamo una ad una tutte queste misure con le problematiche associate.

  La prima cosa da fare e' classificare, individuare, nominare gli oggetti. Nel nostro caso, le monete, sarebbe meglio nominarle con qualche indice che ricordi la coniazione (l'anno, il periodo, il paese, ecc.). Nel nostro caso le monete "moderne" hanno inciso l'anno domini di conio e questo puo' essere una parte del nome, per il resto si potrebbe usare un numero casuale.

  Nel nostro caso utilizziamo il suffisso Internet del paese seguito da un numero di due cifre (esempio DE03, FR13, IT11, ecc.). Per l'anno di conio tutte le monete sono state scelte del 2002 per cercare di azzerare quest'altra variabile.

  Le monete sono state ordinate, per ogni paese, in modo assolutamente casuale e poste nel contenitore che e' lui numerato. I fogli sono singoli e raccolgono un solo paese. Sul quaderno di campionamento andra' descritto tutto il processo di misura ed anche eventuali anomalie rilevate via via.

Un foglio del classificatore, meno la moneta DE13 sotto misura

  Dalla foto notate che manca una moneta, quella sotto misura. UNA ed UNA SOLA moneta deve essere in giro per il laboratorio ed un'altra NON puo' uscire dal contenitore se quella di prima non e' tornata a posto (dovrebbe prevenire inversioni).

  Non e' qui presentata alcuna foto ma le monete sono state raccolte in bar, negozi, giornalai. Dopo aver collezionato almeno 15 monete per ognuno dei 4 paesi sono state tutte pulite accuratamente con acqua, sapone neutro di marsiglia anche con l'aiuto di una spazzola morbida. Utilizzando guanti di lattice le monete sono state prese a 4 o 5 insieme, piene di sapone, e spazzolate sui bordi per ripulire accuratamente la godronatura.

  Sono state poi lavate accuratamente con acqua distillata e poi poste nel bagno ad ultrasuoni nella vaschetta a rete (affiancate e non sovrapposte) e tenute a 30 gradi, 35 KHz, 30W, per dieci minuti. Asciugate accuratamente, lasciate asciugare ancora una giornata fra foglio di carta da filtro. Cosi' come si trovavano fra i fogli, casuali, sono state trasferite nel classificatore gia' numerato.

  Nella vita professionale di un laureato in questa disciplina spesso capitera' di dover ripetere misure su oggetti gia' catalogati, studiati, classificati in precedenza. Uno dei problemi e' di tipo etico-comportamentale: come confrontare le nuove misure con i valori gia' disponibili?

  Non esiste una risposta univoca, bisogna tener conto degli strumenti utilizzati per le prime misure, degli operatori che hanno utilizzato detti strumenti, degli errori relativi ed assoluti, della conoscenza dell'oggetto sotto misura allora ed oggi.

  Di certo non si devono per forza ritenere superiori le nostre misure anche perche' l'oggetto nel tempo puo' essersi modificato. Sarebbe auspicabile uno studio attento di tutte le condizioni di misura passate, un analisi dell'incertezza associata alla vecchia e nuova (singola) misura, di un'analisi chemiometrica dei dati gia' presenti per evidenziare lacune, problemi, singolarita', proprieta', buoni risultati, prima di impostare il nostro piano di campionamento e misura.

  Forse quello che mancava nella misura svolta fino a qualche anno fa (e anche oggi purtroppo) e' uno studio sulla qualita' della misura singola, sull'incertezza associata, sulla rappresentativita'. Tenetene conto per favore.

  Che non sia una misura facile gli studenti lo hanno gia' sperimentato con una precedente esercitazione sul campionamento. Nel caso di una moneta antica si cerchera' di misurare il diametro massimo. Nel nostro caso potra' invece misurare un diametro in un punto facilmente ripetibile.

  La misura deve essere eseguita con uno strumento abbastanza sensibile da mostrare le differenze ma non cosi' sensibile da dover combattere con il rumore strumentale.

  Lo spessore di una moneta antica e' soggetto all'usura del tempo e percio' anche la sua misura deve tener conto di questo problema. Lo spessore puo' essere facilmente misurato con lo stesso strumento usato per il diametro.

  Data una moneta qualsiasi vi sono almeno tre punti di misura, lo spessore massimo (1 in figura), lo spessore minimo (2 in figura), lo spessore in un punto definito (3 in figura). Per la misura di tutti i punti 1, 2 e 3 pero' forse necessita un apposito strumento. Nel nostro caso scegliamo il caso 1.

Una moneta antica da misurare

  Come per il diametro anche per lo spessore discuteremo a lezione altre problematiche associate allo stato di conservazione. La scelta dello stesso strumento pero' aiuta ad ottenere lo stesso numero di cifre significative.

  Questa e' una misura facile, o almeno sembra. Nel nostro esperimento vogliamo leggere le differenze fra monete ancora in circolazione dobbiamo, di conseguenza, utilizzare una bilancia analitica con la giusta risoluzione per evidenziare le differenze. Con la ottima Gibertini utilizzata possiamo scegliere fra la risoluzione di 0.1 mg e 0.01 mg.

Una prima vista della moneta	E con un altra illuminazione
Altra faccia della moneta	Altra faccia, altra vista

  A proposito di questa moneta antica (romana, greca, pontificia, carolingia, ecc.) per chi la riconosce e porta un riferimento certo faremo una domanda a piacere all'esame, e forse 5*10^-1 punti in piu'.

  Vi sono molti metodi per "misurare" la densita' di un oggetto. La definizione di densita' e' Massa/Volume ma ormai sapete che misurare queste grandezze fondamentali puo' essere davvero difficile se si vuole accuratezza, pertinenza, rappresentativita', riproducibilita'.

  Fra le due variabili analizziamo prima i problemi connessi con la misura del volume, vi sono "molti volumi" dato un corpo solido. Per una persona comune il volume e' una misura semplice ma per un laureato Scienze Applicate ai Beni .... tutti gli aspetti devono essere tenuti in considerazione.

  La misura del volume di un solido oltre ad essere complessa per la forma stessa del solido lo anche per le definizioni sui possibili volumi (parliamo di solidi indeformabili, una moneta, un parte di anfora, una scheggia di marmo, un frammento di lancia):

1. Bulk Volume or Envelope Volume: e' il volume del solido compreso tutti i pori sia aperti all'esterno sia interni, comprese anche le fratture ed i difetti. E' anche definito come External Volume. Di solito si misura mediante calcoli geometrici.
2. Apparent Volume: e' il volume del solido misurato escludendo pero' le porosita' che sono aperte verso l'esterno. E' insita la definizione di porosita' come fori di piccolo diametro variabile fra i micrometri ed i 3-4 nanometri. Si puo' misurare per immersione in un liquido sia a pressione ambiente che sotto pressione.
3. Real Volume: e' il volume da cui sono esclusi anche tutte le porosita', raggiungibili dall'esterno di qualsiasi dimensione siano. Sono usati di solito gas nobili sotto pressione per questa misura poiche' riescono a penetrare fra cricche, fratture, ecc.
4. True Volume: ora che abbiamo riempito tutti i pori raggiungibili dall'esterno rimangono ancora da escludere le cavita' (difetti macroscopici chiusi all'interno del materiale) ed i pori che non comunicano con l'esterno (oppure che sono presenti sulle superfici interne delle cavita'). Se troviamo un metodo per valutare il volume occupato da questi quello che rimane e' il True Volume.

  Come al solito a lezione qualche esempio sulla misura dei volumi qui sopra esposti. Ora che sappiamo che sono possibili misure di volume anche molto diverse fra loro in funzione del tipo di materiale, solido, che vogliamo misurare passiamo alla misura della massa.

  Cominciamo subito con ricordare un concetto che si apprende subito sui banchi di scuola, di solito non misuriamo la massa di un oggetto (in g) ma il suo peso (in newton) che e' funzione della posizione dell'oggetto nel sistema di riferimento (terra, luna, Everest, spiaggia del Mar Morto), cioe' della forza di attrazione gravitazionale.

  Per scelta massa unitaria e forza peso unitaria si equivalgono al livello del mare ed addirittura questa uguaglianza e fissata per legge in vari Stati definendo un valore della forza di gravita' media del paese.

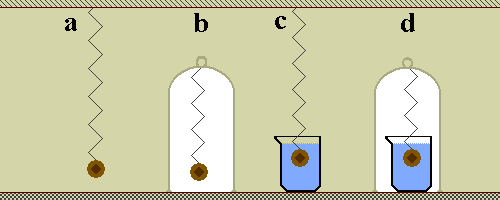Stessa massa pesi erroneamente diversi

  Ed ora entra in campo Archimede, non una ma due volte nelle misura della densita'. Cominciamo dal galleggiamento, secondo il siracusano un corpo immerso in un fluido e' sottoposto ad una forza opposta alla forza peso e pari al peso del volume di liquido occupato dal corpo.

  Nel disegno precedente l'oggetto e' lo stesso, la molla che annulla la forza peso e' la stessa, in due casi nella cupola di vetro e' stato fatto il vuoto, in due casi il corpo e' immerso in un liquido di elevata purezza e di densita' nota.

  Il caso b e' quello che ci fornisce il valore giusto, nel caso a il liquido di cui parla Archimede e' l'aria percio' il peso risulta minore.

  Nel caso c l'oggetto e' immerso in un liquido noto (ma anche nell'aria disciolta) e questo ci permettera' di conoscere il volume che sara' pari alla diminuzione di peso. Nel caso d invece il sistema e' sotto vuoto e dovrebbe essere annullata la spinta prodotta dall'aria, pero' un po' difficile da realizzare.

  In laboratorio per le nostre misure utilizzeremo il modello a per la determinazione del peso dell'oggetto con una bilancia analitica ad 1 piatto con l'opportuna risoluzione per "vedere" le differenze fra gli oggetti. Utilizzeremo invece il modello c per leggere la diminuzione di peso dovuta al galleggiamento di Archimede e proprio la differenza di peso (tenendo conto delle densita' del liquido) ci fornisce il volume immerso. Necessitano le correzioni per la spinta dell'aria che invece non sarebbero necessarie negli altri due casi.

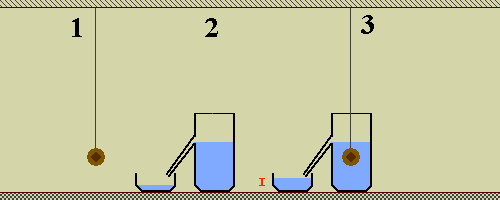Il metodo della corona d'oro di Nimium Hiero

  Un'altra misura del volume e' dovuta sempre ad Archimede (Marcus Vitruvii Pollionis, De Architectura, Liber Nonus) per risolvere un dubbio del suo mentore Nimium Hiero di Siracusa che voleva conoscere la densita' di una corona d'oro forse contraffatta con parti di argento e rame dall'orafo. Curiosamente dopo piu' di 2000 anni noi utilizziamo la densita' come una variabile predittiva in questa lezione sulla chemiometria applicata ai Beni Culturali.

  Effettivamente quanto riportato oggi da moltissimi siti internet non e' plausibile vista la piccolissima differenza di volume (qualche ml) difficile da misurare anche oggi, pero' l'esperimento viene spiegato invece bene da un altro grande scienziato, Galileo mediante l'uso di una leva (anche questa di Archimede) leggendo cosi' qualche grammo di differenza molto piu' plausibile per allora.

  Nella figura precedente viene utilizzato un recipiente di vetro da noi appositamente costruito con una sifone di scarico che finisce in un becker per la raccolta.

  Nel caso 2 il recipiente viene riempito di liquido noto e purissimo con delicatezza ed il becker di raccolta e' posto su di una bilancia tecnica o analitica, il tutto su di un piano antivibrante. Si aggiunge liquido goccia a goccia fino a provocare un traboccamento e poi si azzera la bilancia, tara=0.

  Ora si passa all'immersione dell'oggetto, caso 3 (ottenuta con un sistema lento e motorizzato per non provocare onde sulla superficie del liquido) e si pesa la quantita' di liquido fuoriuscita che sara' pari al volume dell'oggetto conoscendo la densita' del liquido. Non bisogna attendersi una misura molto accurata e consigliamo vivamente almeno 5 prove per ogni oggetto.

  Nel Sistema Internazionale (S.I.) l'unita' di misura della densita' e' il kg/m³ pero' spesso per oggetti compatti si usa invece il g/cm³ con la seguente relazione.

1 g/cm³ = 1000 kg/m³

  Ora questa pagina e' gia' troppo lunga per discutere tutti i casi, le complicazioni, le soluzioni, gli aspetti della misura della densita' con il metodo c visto in precedenza si consiglia di leggere questi tre riferimenti:

1. XS-DichteKit-BA-11780508.pdf (826.521 Bytes) Mettler-Toledo, density determination kit for XS balances. Installazione del kit per la misura della densita' di solidi con formule approssimate e corrette.
2. YDK01_YDK01-0D_YDK01LP.pdf (183.468 Bytes) Sartorius, Density Determination Kit User's Manual. Installazione ed uso del kit, fra l'altro molto simile a quello utilizzato nelle esercitazioni (prodotto* dalla Gibertini per la sua bilancia E50S con risoluzione 0.01 mg), anche qui con le formule.
3. DensityDeterminationManual.pdf (726.291 Bytes) Sartorius, Manual of Weighing Applications, Part 1, Density. 76 pagine di manuale tutte da leggere per conoscere la misura della densita' di liquidi e solidi, sono descritti metodi antichi, approssimati, corretti anche tenendo conto degli errori piu' comuni.

  Per la misura della densita' delle nostre monete avremo bisogno di:

1. Una bilancia analitica con risoluzione 0.1 oppure 0.01 mg con aggiunto il kit di misura della densita' con il metodo di Archimede che pero' abbiamo modificato;
2. Un termometro per la misura, continua, della temperatura dell'aria nell'ambiente dove sono poste le monete, risoluzione almeno 0.5 gradi;
3. Una opportuna quantita' di acqua distillata ultrapura (>15 MOhm) alla stessa temperatura;
4. Un termometro per la misura, continua, della temperatura della soluzione con risoluzione almeno 0.1 gradi;
5. Una serie di fomule come quelle qui sotto (con i fattori di correzione per l'aria e il volume del kit, nel nostro caso 0.99989).

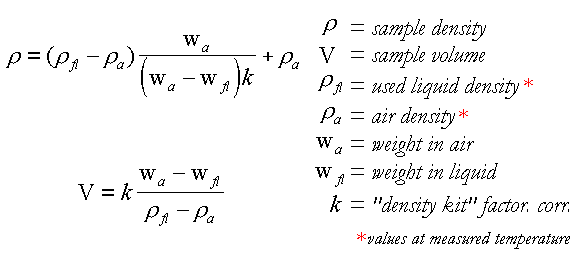Le formule corrette da utilizzare per i calcoli del volume e della densita'

  Ci sono almeno tre effetti della temperatura nella misura della densita'. Il primo e' la dilatazione termica dell'oggetto (solido o liquido) sotto misura, con varie temperature di 5 in 5 gradi si puo' calcolare anche il coefficiente. Aumentando la temperatura il volume aumenta e la densita'; diminuisce (salvo qualche materiale composito).

  Il secondo e' la variazione della densita' del liquido utilizzato per la misura, in questo caso esistono delle tabelle di conversione di cui abbiamo prodotto due file, uno per l'acqua distillata ultrapura non degassata (in formato .123 oppure .WK3) ed un'altro per l'etanolo puro per analisi non degassato (in formato .123 oppure .WK3).

  Il terzo e' l'effetto della temperatura sull'aria percio' sia sul peso in aria sia sui liquidi utilizzati. Anche qui potete utilizzare il file con la tabella per l'aria, alla pressione di 101.325 KPa e umidita' relativa del 70% (in formato .123 oppure .WK3).

  Per facilitare i calcoli abbiamo prodotto un file in cui la prima pagina e' da riempire con i dati rilevati e le altre svolgono i calcoli in automatico. Ricordate che per non danneggiare le formule e' meglio inserire o aggiungere righe sull'oggetto n. 2. Sono disponibili due formati, quello nativo in Lotus 123 ed una conversione in Excel 97 ambedue di circa 250 KBytes.

  Ogni anno agli studenti viene chiesto di produrre un file con i risultati ottenuti dalle misure. Questo e' il file di uno degli anni precedenti. Il file e' mal scritto e sbagliato. A lezione abbiamo visto come scriverne una versione migliore che sara' descrittiva anche fra un anno o due e con la colonna "E" giusta e le colonne "F" e "G" numeriche. Sempre a lezione abbiamo poi scoperto un altro errore che per fortuna e' stato possibile correggere (solo perche' avevano pedissequamente seguito le lezioni sul campionamento).

  I risultati di questo A.A. 2004/2005 sono diversi e riportati in un nuovo file Lotus in cui sono stati corretti anche gli errori di trascrizione recuperando i valori dal quaderno. Il file e' il seguente e ha subito presentato un'altro problema.

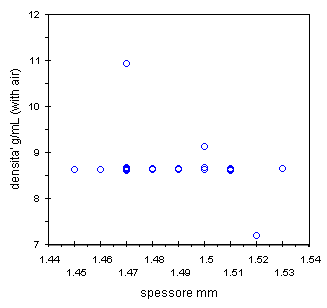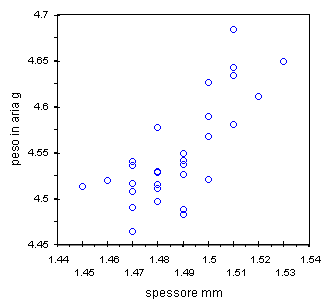
grafico spessore verso peso, sembra normale	grafico spessore verso densita', ecco due problemi

  Nel grafico di sinistra tutto sembra normale, aumenta lo spessore ed aumenta il peso. Si nota l'andamento ma senza outlier. Invece nel grafico di destra sull'asse Y e' riportata una variabile che e' un valore calcolato, non diretto, praticamente un rapporto fra due variabili misurabili. Forse proprio per questo sono emersi due forti outlier.

  Andando a cercare i valori troviamo le monete 95-a et 95-b. Strano che le uniche due monete del 1995 siano gli estremi della distribuzione. Sarebbe meglio ripetere la misura, prima pero' andiamo a rileggere il quaderno di laboratorio (note di lavoro, quaderno di scavo, schede di indagine, quaderno di campionamento, chiamatelo come volete ma riempitelo con cura).

  Troviamo subito l'errore, sul quaderno i due pesi di Archimede sono invertiti per le due monete, cioe' chi ha digitato il file ha commesso un errore. Un errore simile era stato ipotizzato nella gara dei balestrieri.

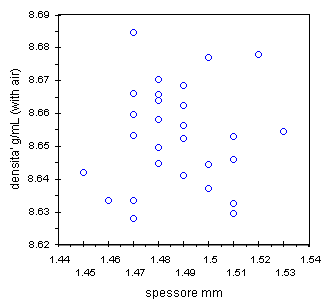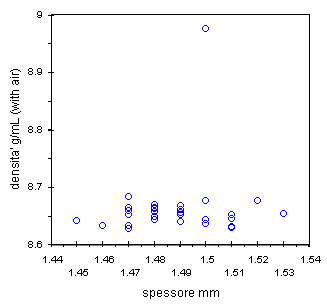
grafico spessore verso densita', corretto ma ....	grafico spessore verso densita', - 1 outlier

  Dopo aver corretto la tabella il grafico di sinistra mostra ora un outlier vero. E' la moneta 98-a che questa volta deve essere davvero misurata prima di definirla un outlier. Poi dopo la nuova misura se si ripresenta l'outlier sara' il caso di indagare sulla moneta, sulla composizione, sulla provenienza, ecc. . Rimuovendo per ora questa moneta si ottiene il grafico di destra che finalmente mostra l'andamento.

  Per gli studenti, ora che avete la matrice dei dati ed il modo per correggerla potete provare a disegnare vari grafici di rappresentazione var-var.

1. matrice dei dati, scaling, analisi multivariata
2. elaborazione mediante chemiometria, classificazione multivariata, della matrice di dati ottenuti dalle misure sulle monete

  L'esercitazione ci permette di chiarire questi concetti. Spesso vengono usati a sproposito da non esperti solo per giustificare la bonta' di una procedura. Usiamo proprio questo set di misure sulle monete per dare qualche definizione, che poi approfondiremo a lezione.

analisi al microscopio, distacco di colore da Madonna lignea dicasi: invasiva, non distruttiva

  Le definizioni sono state spostate, su richiesta di uno studente, alla fine delle slide sulle misure, credo giustamente. Le trovate qui, ricordate come al solito di usare Back o il pulsante del browser per tornare qui

* Bisogna ringraziare il perfetto e puntuale servizio di assistenza della Gibertini che nei primi mesi di vita ha completamente sostituito un E50S che non si accendeva piu' (di certo un piccolo guasto all'alimentazione) ma non crediamo che molte ditte vi fornirebbero una seconda bilancia nuova e con certificato di taratura.

     
Back Page   Home Page   C^© Copyright   We Did It