Kendall's tau test

  Ma mano che si procede nella presentazione dei test non parametrici qualche studente si perde nelle descrizioni e alla fine sembra che tutti i test confrontino le stesse misure e facciano le stesse comparazioni. Non e' questo il caso del Kendall τ che misura la concordanza o la discordanza di piu' coppie di osservazioni.

  La solita citazione storica e' necessaria come sempre per inquadrare il periodo storico dell'autore. Sir Maurice Kendall (1907-1983) ha sviluppato il test che lo ha reso famoso nel 1938 quasi parallelamente ad un lungo lavoro sui numeri casuali, molto meno conosciuto.

  Il test deve essere utilizzato per valutare se due serie di ranks, riferiti ad n. misure, sono correlati fra loro.

  Citando StatSoft: Kendall tau, on the other hand, represents a probability, that is, it is the difference between the probability that in the observed data the two variables are in the same order versus the probability that the two variables are in different orders.

  Oppure, citando Roger Newson at King’s College, London: Kendall's tau_a is the covariance between sign (X_i-X_j) and sign (Y_i-Y_j),.

  Questo test lavora solo con ranks, provenienti da variabili almeno ordinali o con valori binari. Normalmente viene usato per confrontare terapie mediche prescritte allo stesso paziente (vedi Nicola J. Crichton), a confrontare preparazione scientifica e posizione in carriera (vedi riferimento, ed anche questo), ed anche per analizzare la correlazione fra momenti coerenti in una serie temporale (see T. Ferguson, C. Genest, M. Hallin, Kendall's tau for autocorrelation ). Per chi vuole ecco i link a due .pdf da scaricare, Hervé Abdi, and Nicola J. Crichton

  Anche su questo test c'e' qualche piccola confusione. L'ambiguita' e' data dai tre τ citati nei libri, vedremo in seguito. Viene anche definito Kendall tau rank correlation coefficient.

  Non confondete il test con la misura della distanza, gia' conoscete la distanza euclidea, la distanza su meridani e paralleli, la city-block. Dato un oggetto descritto da n. variabili la "Kendall distance" conta quante volte si ha lo stesso valore, in rank, fra le variabili. ). Non e' lo scopo della slide ma trovate qui un riferimento, e qui un altro.

  Studiando un qualsiasi test di correlazione la prima cosa da fare e' capire come funziona e poi applicarlo ad una misura reale che spesso fa saltar fuori i problemi di comprensione. Come al solito un data set reale, in questo caso vediamo se esiste un correlazione fra due esami universitari nel saper valutare la preparazione di un piccolo numero di studenti. Diamo per scontato che gli studenti applicano lo stesso impegno nei due esami (31=30 e lode).

  7 miei studenti hanno superato l'esame nella laurea triennale e nella laurea specialistica. L'ipotesi e' che un esame sia pari all'altro come indicatore di preparazione.

Definizioni:

• la null-hypothesis e' che non ci sia correlazione fra le due serie ordinali,
• cioe' per poter svolgere il test ognuna delle due variabili deve essere trasformabile in rank ordinali, (per esempio un sommelier che valuta 5 vini mettendoli in ordine di qualita'). Non e' necessario che siano numeri, come per il sommelier vanno bene anche giudizi di merito, ottimo, buono, sufficiente, mediocre, nullo. Kendall e' l'unico test che puo' correlare queste variabili,
• al contrario del solito questo test lavora meglio con pochi oggetti, anche soli 4 o 5, e per molti oggetti ha bisogno di una correzione,
• per il test e' necessario che i due set di misure si riferiscano allo stesso oggetto, anche se in tempi diversi,
• il test di Kendall e' di solito chiamato τ, tau test, e produce valori da -1 per una correlazione inversa esatta a +1 per una assoluta correlazione positiva. Il test termina con il calcolo della probabilita' p che misura la significativita',
• non e' richiesto che le distribuzioni ottenute siano esattamente Gaussiane o di Student,
• bisogna far attenzione al bias sulle variabili, se e' presente prima della costruzione dei rank non dovrebbe inficiare molto, ma se la scala e' direttamente ordinale puo' inficiare il test,
• attenzione, il test non prevede e non contempla l'uso di replicati, anzi nella sua versione piu' semplice e' disturbato anche da due "oggetti" che ottengono lo stesso punteggio,
• quando ci si riferisce la test bisogna sempre descrivere attentamente quale dei tre si e' utilizzato e le trasformazioni sulle variabili.

  Viene descritto come τ_a (qualche volta detto gamma), il test semplice quando non ci sono Tied Ranks.

  Invece come τ_b, viene descritto il test che calcola anche la correlazione dovuta ai Tied, ma presenti in piccola misura. Per il nostro esempio e per piccoli campioni e' il piu' usato e di esso presenteremo le formule.

  E' il test piu' complesso, detto τ_c (qualche volta chiamato anche Stuart's test), in cui si tiene conto della correlazione dovuta ai Tied, ma anche della numerosita' delle "misure" che potrebbe autocorrelarsi spontaneamente.

calcoliamo i rank studente voto esame1 voto esame2 rank A rank B an 27 27 4.5 4 fr 23 24 1 2 lu 27 28 4.5 5 pi 30 29 7 6 ri 28 30 6 7 si 24 23 2 1 st 25 25 3 3 combinazioni e segni combinaz. esame1 esame2 sign A sign B an-fr 4.5-1 4-2 + + an-lu 4.5-4.5 4-5 0 - an-pi 4.5-7 4-6 - - an-ri 4.5-6 4-7 - - an-si 4.5-2 4-1 + + an-st 4.5-3 4-3 + + fr-lu 1-4.5 2-5 - - fr-pi 1-7 2-6 - - fr-ri 1-6 2-7 - - fr-si 1-2 2-1 - + fr-st 1-3 2-3 - - lu-pi 4.5-7 5-6 - - lu-ri 4.5-6 5-7 - - lu-si 4.5-2 5-1 + + lu-st 4.5-3 5-3 + + pi-ri 7-6 6-7 + - pi-si 7-2 6-1 + + pi-st 7-3 6-3 + + ri-si 6-2 7-1 + + ri-st 6-3 7-3 + + si-st 2-3 1-3 - -

Calcoli:   Costruiamo la solita tabella, da 5 colonne, nella prima il nome, nella seconda e nella terza i voti (che sono gia' una scala ordinale e potremmo gia' usare questi), nella quarta i ranks calcolati per il primo esame, nella quinta i ranks del secondo esame. I due ranks vengono calcolati sulla colonna, ognuna separatamente.   Nel calcolare i ranks bisogna fare attenzione a mantenere il collegamento fra i due set di misure sull'oggetto.   Ora il test prevede il calcolo (usando i rank values) di tutte le combinazioni possibili, due a due. Quante sono? Ma molte slide fa' abbiamo gia' parlato di combinazioni, permutazioni, etc. combinazioni di n oggetti, p a p   Sono 21 nel nostro caso. Qui a destra abbiamo scritto tutte le possibili combinazioni nella prima colonna, la differenza fra i due rank e' calcolata nella seconda e nella terza colonna, infine i segni ottenuti sono presentati nelle ultime due colonne.   Come detto e ridetto TUTTI questi test e quasi tutte queste slide si possono riprodurre con un foglio elettronico, qui per esempio usando la funzione ©sign(b13) se in b13 c'e' il valore di cui ci interessa solo il segno.   Per calcolare τ dobbiamo contare quanti coppie concordi e discordi si hanno per i segni, per tutte le combinazioni, e poi pesare per il numero di combinazioni e di ties. Con cio' si ottengono appunto valori fra -1 e +1 per τ con la formula seguente (che a lezione leggeremo passo passo): formula completa per calcolare τa   La formula qui sopra e' quella completa e puo' essere usata anche in presenza di un ties, ove invece nel calcolo dei rank ci si trovi di fronte a molti ties sia nella x, (contati qui da tx) che nella y, (contati da ty) dovremmo usare la seguente: formula corretta in presenza di vari ties, τb   Da cui otteniamo il valore τa = 0.762 ed invece il valore di τb = 0.801 che tiene conto del ties 4.5

  Ora data la presenza di un solo ties gli statistici si accapiglerebbero per decidere quale formula usare, a noi invece interessa di piu' sapere se 0.762 e' significativo e percio' se H₀ e' rispettata.

  Come ormai sapete il test di significativita' in tutti i nostri "test non parametrici" e' importante perche' visto il piccolo numero di oggetti coinvolti i valori del test potrebbero solo essere attribuiti al caso.

  Prima di cercare una tabella di valori critici o qualche calcolatore on-line meglio ricordare che se si sospetta una bias positivo (cioe' che aggrega, correla, dati che non lo sono) si possono usare i valori limiti per one-side, se invece non si hanno indicazioni su come potrebbe essere influenzato il test e' meglio usare i valori limiti per two-sides nella opportuna tabella.

  Questa e' una tabella con i valori critici, one-side, per Kendall's test, e' un file .ps buona conversione. Altre si trovano su vari libri di statistica (H.R. Neave et al.).

  Per l'esercizio vediamo che per n=7, il 90% di confidenza ha come limite 0.524, il 95% di confidenza ha come limite 0.619, il 99% di confidenza ha come limite 0.810, ma noi otteniamo 0.762.

  Se il valore di tau e' minore del valore tabulato (τ < C.L.) l'ipotesi H₀ e' accettata. In questo esempio H₀ e' rifiutata al 90% ed al 95% di confidenza, cioe' non possiamo dire che non ci sia correlazione fra i due esami. One side, cioe' siamo quasi certi che comunque i due esami hanno un correlazione positiva.

  Come al solito questa e' la sezione dei calcolatori on-line, eccone uno del Wessa.net del Prof. Patrick Wessa per il cacolo del Kendall's test ed un altro.

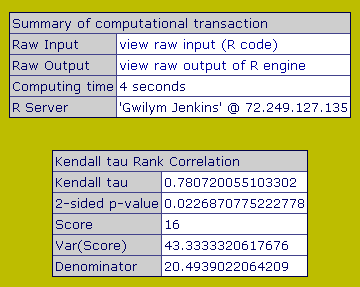Il valore di p=0.023 mostra che la H0 sarebbe rispettata se scegliessimo il 99.97% di confidenza e non il solito 95%

  Il valore calcolato e' un poco diverso dal nostro per il diverso metodo di calcolo del denominatore, cioe' dei tieds, forse usano questa formula.