Friedman test

  Cosa c'entra il famoso economista Milton Friedman (1912-2006), fra l'altro premio nobel nel 1976, con i test statistici? Avete dimenticato che la statistica ed il campionamento nascono nelle scienze sociali? R.A. Fisher la applicava alla eugenetica, W. Gosset la usava nel suo lavoro, uno dei primi software e' stato SPSS.

  Tornando al test, possiamo utilizzarlo per confrontare se piu' di 2 strumenti/operatori/metodi applicati agli stessi "oggetti" forniscono gli stessi risultati tanto da poter sostituire uno con un altro.

  Su questo test non c'e' confusione essendo stato scritto da una sola persona e ben descritto in tre articoli, nel 1937 (The Use of Ranks to Avoid the Assumption of Normality Implicit in the Analysis of Variance), una correzione nel nel 1939 (A Correction: The Use of Ranks to Avoid ....) e nel 1940 (A comparison of alternative tests of significance for the problem of m rankings).

  Un archivio librario, usiamo tre differenti sistemi per controllare l'umidita', posizioniamo questi tre sensori molto vicini fra loro e misuriamo per 15 giorni, alla matrice ottenuta possiamo applicare questo test. Bisogna far attenzione che dato un "oggetto" questo sia misurato nelle stesse condizioni in tutte e tre le prove. Pensate al caso di tre farmaci per la cura di YxYxx, li diamo alla stesse persone? E se confrontiamo quattro professori?

  Questo test puo' essere utilizzato con variabili almeno Ordinali, per distribuzioni abbastanza diverse dalla Gaussiana, con misure fatte in tempi diversi con "risoluzioni" diverse.

  Gli strumenti sono: Toolmex Polmach, 50-100-025N, vernier micrometer, 0-25 mm, 0.01 mm, A=usato, B=nuovo; Mitutoyo, mod. 293812, MDC lite micrometer, 0-25 mm, 0.001 mm.

  Ormai il data set non necessita di una descrizione. Gli oggetti sono le famose provette da centrifuga e misuriamo il diametro a 10 mm dal fondo con tre micrometro che forniscono, due identici, una risoluzione di 0.01 mm, ed il terzo di 0.001 mm. Un solo operatore addestrato.

Definizioni:

• la null-hypothesis e' che i 3 o piu' strumenti diano risultati equivalenti, oppure che i tre trattamenti siano equivalenti, oppure che i tre operatori siano intercambiabili
• definiamo groups gli strumenti/metodi/trattamenti e items gli oggetti/pazienti/posizioni, di conseguenza,
• e' richiesto che i tre groups siano indipendenti e che le scale siano almeno ordinali (opp. ad intervallo opp. a rapporti, ma non binari),
• e' richiesto che l'applicazione di un metodo/strumento/trattamento non disturbi la popolazione,
• per un test attendibile un valore minimo per gli items puo' essere fra 5 e 7, con valore massimo anche oltre la soglia di Student,
• il test puo' essere usato anche per misure ripetute, gli elementi della matrice possono essere anche medie o mediane di piu' misure, possono anche essere indici di qualita' trasformati in scala ordinale,
• non e' richiesto che le distribuzioni ottenute siano Gaussiane o di Student, o seguano una altra distribuzione nota,
• il numero di items deve essere superiore a quello dei gruppi, almeno di un fattore 2,
• il test puo' (o deve!) essere utilizzato tutte le volte che One/Two Way Anova non e' applicabile,
• i gradi di liberta' del test sono groups-1.

  Nell'articolo originale M. Friedman non dava una sigla per il test, vari autori lo citano come χ_r² , oppure come Q , od anche come T₁ (senza dimenticare T₂ se si vuol usare la distribuzione di Fisher per trvare la significativita').

items microm. B microm. A microm. Digit. rank B rank A rank D I 14.84 14.85 14.808 2 3 1 II 14.81 14.82 14.798 2 3 1 III 14.84 14.84 14.809 2.5 2.5 1 IV 14.84 14.83 14.827 3 2 1 V 14.75 14.78 14.750 1.5 3 1.5 VI 14.80 14.85 14.824 1 3 2 VII 14.74 14.76 14.758 1 3 2 VIII 14.86 14.86 14.836 2.5 2.5 1 IX 14.83 14.85 14.846 1 3 2 X 14.72 14.74 14.720 1.5 3 1.5 XI 14.73 14.76 14.751 1 3 2       Σri 19 31 16       average 1.727 2.818 1.455       (22-Σri)2 9 81 36

Calcoli:   Per prima cosa costruiamo una tabella da 7 colonne, la prima e' il nome dell'items, la seconda/terza/quarta sono i valori misurati per il gruppo A/B/D nell'ordine. Le altre due sono i ranks.   Particolarita' del test e' il calcolo dei ranks "di riga" cioe' fra i gruppi con il solito metodo anche per i ties. Controllate che la somma totale sia pari alla formula qui sotto. la somma di tutti i ranks e la loro media aritmetica   Gia' guardando i risultati si nota qualche differenza: il valore atteso per la somma dei rank di gruppo sarebbe 3*((11*(3+1))/2)= 3*22 = 66 e la media attesa dovrebbe essere (3+1)/2 = 2.   Sembra che l'ipotesi H0 non sia rispettata! ma per controllare che questo non sia dovuto al caso bisogna confrontare il risultato con una distribuzione note ed ottenere la significativita'. Qui iniziano i problemi, l'autore nel suo lavoro cita χ2 ma qualche anno dopo anche F di Fisher. F di Fisher, piccoli campioni, n*k<35

  Se stiamo nel caso n*k<35 usiamo la F di Fisher con la formula gia' vista ed otteniamo nell'esempio visto F_r=126. Ove fossimo invece nel caso n*k>40 sarebbe meglio usare per i calcoli χ_r²e per le tabelle di significativita' il χ².

  Nel nostro caso, con F_r, data l'ipotesi H₀ che non vi sia differenza fra i gruppi ora dobbiamo calcolare quanto e' significativo il valore trovato. Come al solito i valori di significativa' sono al 90%, al 95%, al 99% a seconda di quanto accettiamo di errore sulla H₀.

  Una tabella con i valori di Fisher la trovate su questo .pdf del Prof. L. Soliani, a pagina 60/61 (c'e' anche una bella descrizione). Oppure la trovate qui se non e' raggiungibile. Per l'esercizio vediamo che per k=3, n=11, il 95% di confidenza ha come limite 72, ma noi otteniamo 126. L'ipotesi H₀ e' rifiutata.

  Sono disponibili almeno due calcolatori-on-line per il Friedman test. Come al solito sul Vassar College: Friedman k=3, et Friedman k=4 (ma queste pagine hanno qualche problemino di calcolo con alcuni browser, non e' colpa mia!). Un altro calcolatore online lo trovate qui, ma e' ancora peggio sui vari browser.

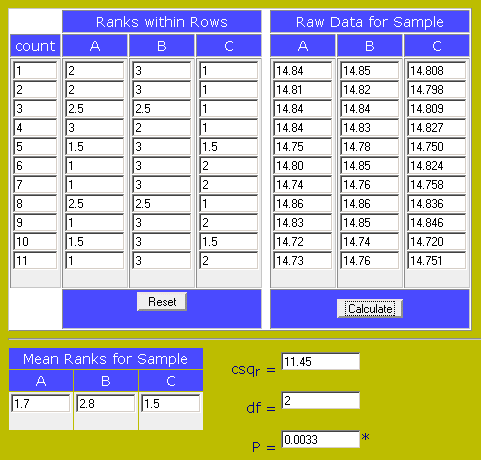Il valore di p=0.0033 mostra che la H0 sarebbe rispettata se scegliessimo lo 0.3% di confidenza e non come al solito il 95% o il 99%

  Fate attenzione alla scritta "Mean Ranks for Sample" qui sopra, se avete letto i vari link scoprite che questo calcolatore on-line usa χ² e non F_r per il calcolo della significativita' !!

  Aggiungiamo un link ad un altra descrizione del test in questione, del NIST.

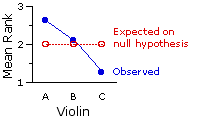
  Non e' lo scopo di queste slide di enumerare e spiegare tutti i test di correlazione (e poi prima di scrivere di una cosa bisognerebbe conoscerla!), percio' a chi e' interessato a questo test ecco un altro link.

  Ma allora bisogna citare anche un altro test molto simile, quello descritto da William Gemmell Cochran (1909-1980).

  Come al solito il grafico che si puo' produrre con questo test aiuta alla sua comprensione.