Spearman's Rank Correlation

  Questa volta la citazione storica e' davvero necessaria, bisogna inquadrare il periodo storico di nascita del test. Charles Edward Spearman (1863-1945) ha sviluppato il test, nel 1904, per testare statisticamente se due set di dati, diciamo due distribuzioni, sono fra loro correlate. Trovate citato il test nei libri anche come "Spearman Rank-Order Correlation Coefficient"

  Il test deve essere utilizzato per valutare se esiste una relazione fra due serie di misure, e misurarne l'affiatamento.

  Su questo test c'e' qualche piccola confusione. L'ambiguita' e' nel metodo di calcolo e nell'applicazione alle misure come anche nell'interpretazione dei risultati, qui daremo l'interpretazione originale e comunque anche alcuni web-riferimenti. Qualche autore lo cita anche al contrario come test di indipendenza fra due variabili. I riferimenti: A pragmatic Approach, Rank-Order Correlation, Spearman's rho.

  Questo test puo' essere utilizzato con variabili almeno Ordinali, ma anche per distribuzioni abbastanza diverse dalla Gaussiana e per set di misura con numerosita' diversa.

  Non fate confusione! La correlazione di Spearman e' definita come una relazione monotonica dove Y cresce o descresce continuamente in funzione di X. Questa correlazione puo' essere analizzata sostituendo ai singoli valori di X e di Y la loro posizione nell'insieme delle osservazioni. Sembra tanto il test ma e' un altra cosa

  Due variabili misurano, con scale almeno ordinali, una serie di oggetti, anche virtuali, e vogliamo essere certi che la varianza di una variabile NON sia correlata con la varianza dell'altra variabile.

  Sarebbe meglio se gli oggetti fossero estratti casualmente dalla popolazione, che nessuna delle variabili sia affetta da bias, che gli eventuali sampling desings siano ben condotti.

  Il data set a disposizione e' composto da 112 interviste ma ne sono state estratte solo 13 mediante un campionamento simple random sampling without replacement. Non apriamo qui la discussione sul dominio di studio, sull'area di interesse, etc..

Definizioni:

• la null-hypothesis e' che non ci sia covarianza fra i due set di misure. Cioe' che i due set non siano dipendenti (se fosse possibile calcolare R² sarebbe =0),
• per la soluzione del test si usano i ranks, calcolati per ogni distribuzione, e si ipotizza che la loro differenza sia solo dovuta al caso,
• come tutti i test non parametrici ci vuole un discreto numero di misure per confrontare le due distribuzioni. Di solito si usa un numero totale compreso fra una decina e la soglia di Student,
• per il test e' necessario che i due set di misure si riferiscano allo stesso oggetto, possono anche misurare un "oggetto nascosto"*, una proprieta', ecc.,
• non e' richiesto che i due set siano ottenuti contemporaneamente ma le scale devono essere almeno ordinali (opp. ad intervallo opp. a rapporti). La numerosita' dei due set di misura deve essere uguale n_i=n_j,
• il test di Spearman e' di solito chiamato ρ, rho test, e produce valori da -1 per una correlazione inversa esatta a +1 per una assoluta correlazione positiva. Il test termina con il calcolo della probabilita' p che detta correlazione sia significativa (ad una o due code),
• non e' richiesto che le distribuzioni ottenute siano esattamente Gaussiane o di Student, anche un piccolo bias su una variabile non disturba il test se omoscedastico,
• attenzione, poche misure ed un campionamento non rappresentativo producono con questo test errori di tipo II.

  *un esempio che potete leggere qui e' il costo di una bibita in funzione della distanza da un "evento" (una partita, un concerto, ecc.), l'oggetto nascosto e' l'ingordigia di chi sfrutta una rendita di posizione.

altezza n.scarpa rank A rank B d2 1.58 37 1.5 2.5 1 1.58 38 1.5 5 12.25 1.60 36.5 3 1 4 1.62 39 4 7.5 12.25 1.63 37 5 2.5 6.25 1.65 38 6 5 1 1.69 38 7 5 4 1.74 44 8 10.5 6.25 1.78 43 9 9 0 1.79 39 10 7.5 6.25 1.88 44 11 10.5 0.25 1.91 46 12 13 1 1.92 45 13 12 1   summa 91 91 55.5

Calcoli:   Per prima cosa costruiamo una tabella da 5 colonne, la prima e la seconda sono le due variabili, le altre tre piene di zeri. Mettiamo in ordine crescente la tabella per la prima colonna, nella terza ora calcoliamo e scriviamo i rank collegati alla prima colonna. Riordiniamo ora la tabella per la seconda colonna, ora nella 4 colonna calcoliamo e scriviamo i rank collegati alla colonna 2. Anche se non necessario ora vari autori riordinano per la terza colonna (il rank di A). Finalmente nella colonna 5 calcoliamo d2=(rankA-rankB)*(rankA-rankB) per ogni oggetto.   Nel calcolare i ranks bisogna fare attenzione sia a mantenere il collegamento fra i due set di misure e l'oggetto, sia alla somma dei ranks che deve dare il valore calcolato con la solita formula. Agli estremi si possono ottenere due casi. Una perfetta correlazione, evidenziata dai ranks rank A  1  2  3  4  5  6  7  8  9 10 11 12 13 Σd2 rank B  1  2  3  4  5  6  7  8  9 10 11 12 13 0.0 I ranks evidenziano una correlazione inversa rank A  1  2  3  4  5  6  7  8  9 10 11 12 13 Σd2 rank B 13 12 11 10  9  8  7  6  5  4  3  2  1 728   Come gia' detto il test prevede che per la correlazione diretta si ottenga il valore ρ=+1 , e per la correlazione inversa, esatta, ρ=-1. Ora bisogna trovare una formula matematica che, dato il numero di oggetti (n), e data la somma dei quadrati (d2) appena calcolata, ci porti a questo risultato. Qualche prova con 3, 4, 5 oggetti ci porterebbe a generalizzare la formula: calcolo di rho, dati n et di   Data la formula nel nostro caso abbiamo ρ (rho) = +0.8475 che dobbiamo interpretare. Il valore sembra vicino al massimo, +1 e percio' dovrebbe indicare una accentuata correlazione fra le due misure.

  Data l'ipotesi H₀ che non vi sia covarianza fra le due misure ora dobbiamo calcolare quanto e' significativo il valore trovato. Come al solito i valori di significativa' sono al 95%, al 98%, al 99% a seconda di quanto accettiamo di errore sulla H₀.

  La maggior parte dei testi oggi consigliano la Boostrap Analysis o Permutation Analysis ma i vecchi metodi gia' visti di confronto dei dati con una tabella si possono ancora usare. Trovando la tabella giusta, questa? (Sussex University).

  Scelto il 95%, cioe' 0.05 in tabella, dato n=13 nel nostro caso (in tabella scegliamo lui od il piu' piccolo, 12) troviamo 0.591 che ci da quale potrebbe essere ρ dovuto al solo caso statistico, dato che il nostro valore e' ben superiore l'ipotesi H₀ e' rifiutata. Lo sarebbe anche per il 98% ed il 99% nel caso in esame.

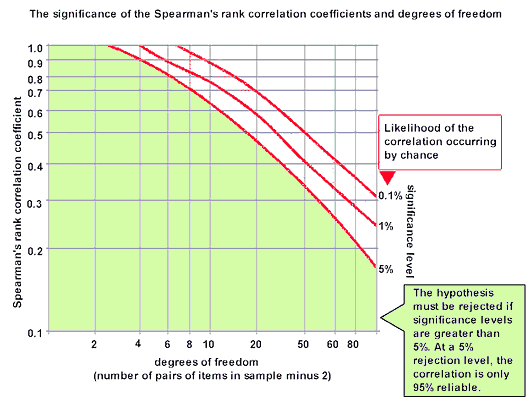Un bel grafico per il calcolo della significativita' di ρ. Fate attenzione che la scala X e' logaritmica e misura i gradi di liberta'. Preso qui.

  Sono disponibili almeno due calcolatori-on-line per il Spearman rank test. Questo calcolatore lo trovate presso il solito Vassar College, anche l'altro calcolatore e' su di un sito famoso, Wessa.net del Prof. Patrick Wessa.

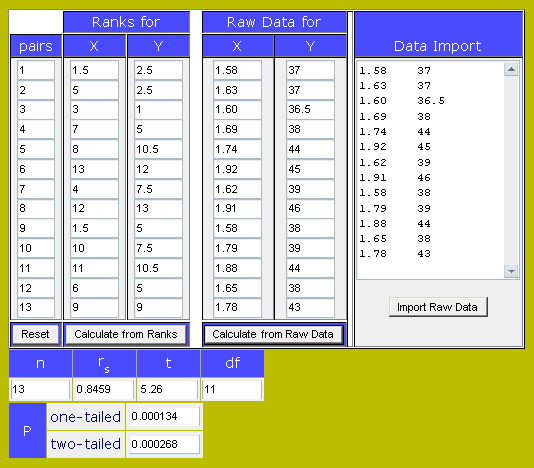La solita confusione, qui ρ viene chiamato rs. Anche il valore e' un poco diverso da quello calcolato con la formula perche' e' corretto tenendo conto dei gradi di liberta'

  Se la vostra subnet e' compresa in quelle che hanno accesso alla risorsa potete anche visualizzare il bellissimo articolo: Jerrold H. Zar, Significance Testing of the Spearman Rank Correlation Coefficient, Journal of the American Statistical Association, Vol. 67, No. 339 (Sep., 1972), pp. 578-580, con le formule e le correzioni. Io ne ho una copia.

  Non e' necessario che i due set di dati (cioe' le due variabili) siano due misure dello stesso oggetto. Proprio per questo il test e' una vera stima della correlazione, come il Pearson ed il Kendal test.

  Per esempio nel caso del campionamento delle nostre provette potremmo correlare i 13 valori prodotti dal simple random sampling with replacements con i valori prodotti dal systematic sampling with a random start.

  L'interpretazione dei risultati e' ben piu' complessa, praticamente stiamo confrontando le due distribuzioni per come siamo riuscite a leggerle attraverso i due campionamenti. Per il fondo della provetta sappiamo trattasi di una bimodale e se i campionamenti hanno fatto un buon lavoro l'ipotesi H₀ non dovrebbe essere soddisfatta.

  Pero' molti autori non usano il test di Spearman per questo confronto ma bensi' il Kendall τ test, vedremo fra qualche slide.