Kruskal-Wallis test

  Un altro test non parametrico prodotto da William Henry Kruskal (1919-2005) e dal suo professore Wilson Allen Wallis (1912-1998) che viene utilizzato per confrontare piu' serie di misure provenienti da un campionamento effettuato su di una popolazione. Si possono incrociare confronti i risultati di piu' strumenti di misura, piu' procedure analitiche, piu' operatori, ecc. .

  Su questo test non c'e' confusione, e' anche definito Kruskal-Wallis one-way analysis of variance by ranks. Se c'e' qualche ambiguita' nei cento riferimenti che trovate e' su "cosa" testa.

  Anche qui bisogna far attenzione che gli oggetti siano estratti casualmente dalla popolazione, che non ci siano effetti di bias, che gli eventuali sampling designs siano ben condotti.

  Questo test puo' essere utilizzato con variabili almeno Ordinali, ma anche per distribuzioni abbastanza diverse dalla Gaussiana e per set di misura con numerosita' diversa.

  Il data set necessita di una descrizione per capire a cosa si applica il test. Gli oggetti sono le famose provette da centrifuga e misuriamo il diametro a 10 mm dal fondo con un micrometro che fornisce una risoluzione di 0.01 mm. Abbiamo a disposizione due micrometri e tre studenti come si vede dalla tabella qui sopra. In inglese, we testing the equality of the central tendency of the samples coming from a populations. Cioe' testiamo uno dei valori che misurano il valore centrale, il valore piu' probabile. Molti autori individuano questo valore nella mediana, altri nella media aritmetica, credo nessuno nella moda, media geometrica, etc.

Definizioni:

• la null-hypothesis e' che i 3 o piu' campioni estratti da una singola popolazione abbiano la stessa central tendency e la stessa shape of distribution della distribuzione,
• di conseguenza,
• e' richiesto che i tre set di misure siano indipendenti e che le scale siano almeno ordinali (opp. ad intervallo opp. a rapporti),
• come tutti i test non parametrici ci vuole un discreto numero di misure per confrontare le due distribuzioni. Di solito si usa un numero totale compreso fra una decina e la soglia di Student.
• non e' richiesto che le distribuzioni ottenute siano Gaussiane o di Student, o seguano una altra distribuzione nota,
• non e' richiesto che la numerosita' delle due distribuzioni sia uguale (ma viene meglio se sono simili).
• alcuni statistici prevedono un valore minimo per ogni campionamento pari a 5, ma altri danno un limite piu' alto.
• questa volta i gradi di liberta' sono facili da calcolare df = n.di.gruppi - 1 . cioe' nel caso in esame df = 2
• il test deve essere preferito al One Way Anova almeno per N < 30 e quando le distribuzioni non sono esattamente gaussiane, Anova e' troppo vulnerabile alle deviazioni dalla normalita' di anche solo uno dei set di dati.

  Ricapitoliamo, abbiamo 3 o piu' campionamenti sulla stessa popolazione con ognuno un numero simile di misure e cerchiamo se mostrano similitudine. Il test e' normalmente definito con la sigla " H-test " e qui ipotizziamo che NON ci sia differenza fra i tre set.

count sample rank 1 14.63 1 2 14.64 2.5 3 14.64 2.5 4 14.66 4 5 14.67 5.5 6 14.67 5.5 7 14.68 8 8 14.68 8 9 14.68 8 10 14.70 10 11 14.71 11 12 14.72 13.5 13 14.72 13.5 14 14.72 13.5 15 14.72 13.5 16 14.73 17 17 14.73 17 18 14.73 17 19 14.74 19.5 20 14.74 19.5 21 14.75 21.5 22 14.75 21.5 23 14.76 23.5 24 14.76 23.5 25 14.77 25.5 26 14.77 25.5 27 14.78 27.5 28 14.78 27.5 29 14.79 29 30 14.80 30 31 14.81 31.5 32 14.81 31.5 33 14.85 33

Calcoli:   Anche in questo test il calcolo inizia con la messa in ordine crescente di tutti i valori dei tre campionamenti (tutti con 11 misure, meglio cosi'), come potete vedere qui a sinistra. La terza colonna mostra il rank calcolato come al solito.   Questa volta ci sono vari Tied Ranks che si dividono la posizione da loro occupata in modo che ogni campionamento non tragga beneficio dalla posizione. Ma ormai sappiamo come calcolarli.   Il calcolo inizia con la somma dei rank per ogni campionamento, con la media di gruppo, calcoliamo poi la somma di tutti i rank e la media generale. Come riferimento e' mostrata anche la mediana di gruppo. Computed on Rank    Valeria   Marianna   Vincenzo  mediane (of values) 14.74 14.77 14.67 sum of ranks, Ri 211.5 265.5 84.0 average of ranks 19.23 24.14 7.64 sum of all ranks 561.0     average of all ranks   17.0   degrees of freedom     2   Prima di continuare un piccolo controllo. La somma di tutti rank deve essere uguale al valore della formula seguente, se avete calcolato bene tutti i ranks. somma di tutti gli interi da 1 ad n   Il calcolo che sottende questo test e' l'uso di una misura delle dispersione per ogni gruppo e compararla con quella totale. Piu' avanti troveremo un test parametrico che fa davvero l'analisi delle varianze per piu' gruppi e che spesso viene confuso con questo.   In inglese si definisce il termine between-groups sum of squared deviates che e' la parte principale di questo test. Calcoliamo la differenza (al quadrato) fra le medie e moltiplichiamo per il numero di misure, per ogni gruppo, Valeria, Marianna, Vincenzo.  SSbg(R)=  (19.23-17.0)2*11 = 54.57  SSbg(R)=  (24.14-17.0)2*11 = 560.20  SSbg(R)=  (7.64-17.0)2*11 = 964.45   Ora bisognerebbe enumerare le possibili combinazioni di n1, n2, n3 oggetti in tre gruppi e calcolare la media dei rank per poter pesare la media da noi ottenuta.   Ma questo non e' un corso di statistica e credo sia meglio passare alla formula per il calcolo di H (where n=total number of mesures, ni=number of measures for group i, Ri=sum of ranks for group i). Kruskal-Wallis, H computation   Il valore ottenuto H=16.89 va ora confrontato con una tabella di valori limite scegliendo in questo caso quella per 2 gradi di liberta' e per il valore di probabilita' definito in precedenza, per esempio 95% (p=0.05).

  Per il calcolo del test, almeno nei casi di 3 o 4 gruppi, sono disponibili vari calcolatori on-line, prima leggete la descrizione del H-test sul Vassar College, Poughkeepsie, New York, e poi provate il loro calcolatore per 3 gruppi, oppure per 4 gruppi.

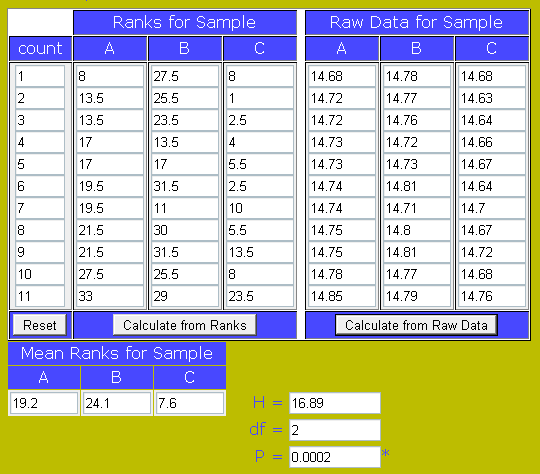Questa volta siamo interessati solo alla differenza fra i gruppi. Avevamo impostato una H0 vera al 95% di probabilita', p=0.05. Leggendo la probabilita' ottenuta i nostri tre gruppi sembrano provenire dalla stessa popolazione e non mostrano differenze fra loro anche per p=0.01

  Vari test statistici, anche alcuni non parametrici, possono essere studiati anche per via grafica. Il valore di probabilita' NON puo' essere sostituito da un grafico e l'ipotesi H₀ si conferma solo con i calcoli, ma spesso un grafico aiuta la comprensione del fenomeno.

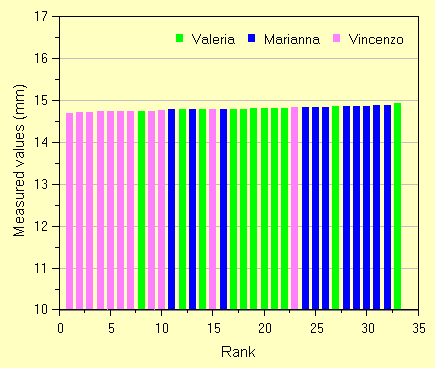Barre in sequenza, opportuna scala sull'asse Y e scelta dei colori per evidenziare come si dispongono i gruppi nel rank order.

  Dal grafico si vedono due cose: a) i valori poco diversi della misura (asse Y) sembra senza outliers; b) la sovrapposizione fra i gruppi con pero' una "propensione" di Vincenzo a ottenere valori bassi e Marianna al contrario.

  Un test molto simile e' quello sviluppato dall'economista Milton Friedman. La prima parte del test e' molto simile a quello appena visto e nono solo gli studenti tendono a confonderli. Ne parleremo in una slide apposita.