Pr. G. Visco; La misura, definizioni, parametri, la qualita' della Misura (un esercizio, la dispersione, spread)

Rome University, La Sapienza Chemistry Department Rome, Italy, Europe	Dr. Giovanni Visco concetto di misura e sua qualita', parametri, problematiche gennaio 2003	Corso di Laurea in: Scienze Applicate ai Beni Culturali ed alla Diagnostica per la loro Conservazione Corso di laurea in: Chimica Ambientale
previous slide, 33	all lessons, these slides index	next slide, 35

Esempi delle definizioni gia' viste, una gara di balestrieri medioevali; la dispersione [spread]

In questo esempio si dovrebbe parlare di accuratezza, precisione, ripetibilita', riproducibilita', errore, stabilita' ed il nuovo concetto di dispersione. Per farlo abbiamo scelto di rappresentare un torneo che si svolge in molte citta' del centro Italia e della Sardegna.

Iniziamo con una foto dei balestrieri di Cortona, ricavata dal loro sito internet. In essa possiamo notare la balestra di cui si parlera' in seguito, il dardo, l'operatore, il contesto ma non il bersaglio che e' quanto ci serve per semplificare i concetti fino a qui esposti.

L'idea di usare una giostra dei balestrieri e' di uno studente. Abbiamo visto varie pagine che spiegavano, in breve, questi concetti usando fucili o altri strumenti di offesa (support Emergency). Quello che ne risulta pero' non ha quasi nulla a che vedere con un torneo vero, ci e' utile solo per chiarire i concetti di metrologia.

Seppur un poco preoccupati per la loro incolumita' ........, ecco i soliti uccellini della riga di separazione.

La gara, dati grezzi

Ma passiamo ai bersagli. Ci poniamo DIETRO al balestriere e con una macchina fotografica e teleobiettivo otteniamo le tre serie di foto qui riportate. Dopo un facile processo di digitalizzazione possiamo calcolare le coordinate, in pixel, di dove si sono piantati i dardi.

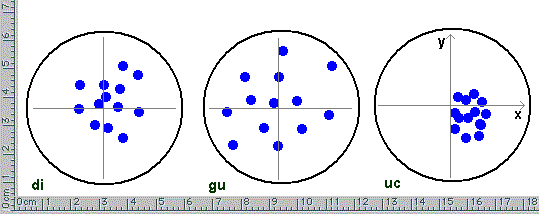
sinistra, X	78	78	95	99	123	103	139	105	107	118	120	123	137
sinistra, Y	84	108	124	103	137	84	111	96	127	106	88	65	74
centro, X	226	232	244	251	264	278	274	279	282	296	302	331	328
centro, Y	111	144	76	99	128	145	103	76	50	100	128	65	114
destra, X	454	458	454	457	466	473	481	474	468	485	466	478	480
destra, Y	129	117	112	96	100	94	101	111	118	114	137	136	124

Vediamo quale delle definizioni gia' viste si adatta alla foto dei bersagli qui sopra.

ripetibilita', a breve termine, dato che i centri sono ottenuti con la ripetizione di 13 lanci; ma i 13 dardi sono diversi, seppur costruiti per essere simili, ripetibilita' del singolo armigero/balestra;
ripetibilita', a lungo termine, se studiamo le tre serie di lanci dello stesso balestriere; ma questa volta i dardi diversi sono 39 ed anche le condizioni ambientali possono cambiare;
riproducibilita', se la stessa balestra fosse usata da piu' balestrieri. Tre sole serie di ripetizioni non bastano pero' per calcolare l'affidabilita'; ma rimane il problema dei dardi della variabilita' ambientale e di qualche regolazione al mirino che ognuno potrebbe fare;
precisione, NO, tutto dovrebbe essere uguale, il dardo, il vento, la balestra, l'armigero. Dato che questo non e' il caso non possiamo parlare di precisione.

Invece si tratta di tre balestrieri diversi, Dionisio, Guidobaldo, Uccione, ognuno ha usato la sua balestra, ed hanno ripetuto tre serie di lanci, alternandosi sul tenone.

Questa e' la seconda serie di lanci, con sotto le coordinate (in pixel) dei punti colpiti.

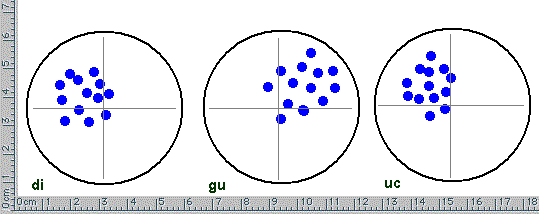
Dionisio, X	60	61	64	69	78	78	87	88	94	98	100	105	108
Dionisio, Y	84	99	121	73	79	109	93	122	72	98	84	114	94
Guidobaldo, X	268	280	280	288	293	303	302	310	310	317	323	335	333
Guidobaldo, Y	87	118	70	103	83	109	67	52	87	72	101	88	70
Uccione, X	407	408	419	420	430	428	429	429	434	444	451	446	445
Uccione, Y	83	96	98	68	55	71	85	115	97	68	77	91	108

Questa e' la terza serie di lanci, con sotto le coordinate (in pixel) dei punti colpiti. Notiamo che il tempo passa, alla fine il singolo balestriere avra' lanciato 39 dardi, il pubblico rumoreggia, incomincia a calare il sole, bisognera' trovare dei metodi numerici, statistici, che studino il singolo set (da 13 valori) di lanci e la serie completa da 13+13+13.

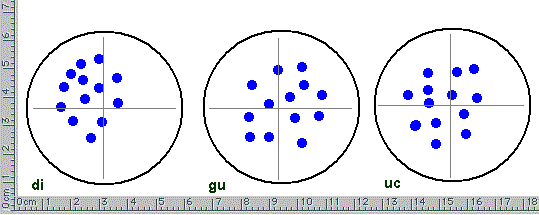
Dionisio, X	60	64	71	73	81	83	85	90	99	102	99	117	117
Dionisio, Y	106	86	73	120	63	79	98	137	58	121	88	77	102
Guidobaldo, X	249	250	252	269	268	277	289	301	295	301	303	322	319
Guidobaldo, Y	116	137	85	137	103	70	97	66	117	142	84	94	116
Uccione, X	407	415	436	436	428	427	427	451	457	473	476	464	466
Uccione, Y	94	125	143	122	103	90	72	94	71	68	97	113	133

Ora che abbiamo calcolato i singoli punti troviamo uno stimatore della riproducibilita' di ogni singolo set di lanci. Ricordate quanto detto sulla Precisione, ci piacerebbe poter stimare questa, ma ...

Dispersione

Dobbiamo trovare un metodo matematico di calcolo che ci permetta di trovare chi ha una riproducibilita' maggiore, chi poco meno e chi e' il peggiore dei tre.

Questo potrebbe essere un metodo. Per ogni set di 13 valori suIl'asse X calcoliamo la differenza fra il valore massimo e minimo, definiamo cosi' la dispersione [spread] che ci misura quanto sono disaggregati i valori ottenuti. Ripetiamo lo stesso sull'asse Y.

Tab.1

Tutti i dati, in pixel, che si trovano sotto le tre foto precedenti sono stati trascritti in un foglio elettronico (Lotus 123) e utilizzando le funzioni del foglio sono stati calcolati il minimo, il massimo, la differenza, ecc. Il file con i dati e le formule e' disponibile in due formati, Lotus 9.8 (balestrieri.123) e Lotus 3.x (balestrieri.wk3).

Riferendoci alla prima cella in alto a sinistra (A5 "concetto di Disp...."), le formule utilizzate sono:

in B23, @MIN(B9..B21)
in B24, @MAX(B9..B21)
in B26, +B24-B23
in B27, +B26+C26
in B28, +B27+C27+H27+I27+N27+O27

Il modello matematico

L'idea era quella di trovare una formula matematica, un modello, che fosse utile a descrivere e studiare il fenomeno con dentro (al modello) qualche stimatore che ci dica chi e' stato piu' preciso (volgarmente parlando). Osservando attentamente i risultati si evidenziano almeno tre punti:

il valore in B26 (valore 61) e' effettivamente la dispersione dei risultati dei lanci, su X, e' un valore estremo che non viene quasi mai usato per descrivere una distribuzione. Con questa misura si terrebbe conto anche di un dardo difettoso che si e' piantato sul muro del palazzo a 13500 pixel di distanza dagli altri 12!
il valore somma in B27 (valore 133) e' teoricamente errato, per eccesso, in quanto definisce il perimetro/2 di un rettangolo in cui cadono tutti i lanci, ma le distribuzioni sono quasi sempre ellissi/cerchi, piu' raccolte. Altra possibilita' sarebbe B26*C26 cioe' l'area del rettangolo pero' moltiplicando cosi' gli effetti di sovrastima. Altra possibilita' ancora sarebbe sqr(b26*b26+c26*c26), cioe' il valore della diagonale del rettangolo
nonostante questo, B27, dispersione ΔX+ΔY, ci da molte indicazioni. Uccione ha fatto ottimi tiri all'inizio ma ha sofferto la stanchezza tanto che nell'ultimo set e' stato ben superato da Dionisio. Dionisio mantiene costante la sua riproducibilita' per tutta la gara. Guidobaldo e' il meno riproducibile, sempre, ma e' piu' ripetibile a lungo termine tenendo conto del peggioramento di Uccione.

Potremmo ipotizzare invece l'uso di una sola balestra con cui si alternano tutti e tre i balestrieri. In questo caso potremmo, dopo 117 lanci, incominciare a fornire qualche indicazione sulla riproducibilita', sull'affidabilita', sulla robustezza. Se poi chiamiamo anche tre astanti, e dopo una breve descrizione della tecnica di lancio, gli facciamo ripetere le 117 prove potremmo definire anche la stabilita' della balestra.

A proposito avete idea se "La Balestra" e' metrologicamente robusta oppure stabile? Una risposta a lezione.

previous slide, 33

all lessons, these slides index

next slide, 35