Chi-quadro test

  Ormai ci siamo abituati, su questi test statistici ci sono ambiguita' sia sui nomi, sia sulle procedure utilizzate, sia sulle formule. Questa volta ci siamo superati, alcuni mettono il chi-quadro nei test parametrici, altri nei non parametrici. Come vedete in queste slide e' finito qui.

  Il χ² test e' dovuto ad uno dei padri della statistica, K. Pearson, mi sembra nel 1901, e sulla sua logica si sono poi basati tanti altri test parametrici.

  Dato che il test e' basato sulle frequenze attese ed osservate possiamo definire come precondizioni:

• trattasi di un campionamento di una ipotetica popolazione di cui e' nota la composizione
• che le uscite siano mutamente esclusive (le due facce di una moneta)
• che si lavori su di una sola variabile di misura, pero' accettando anche scale nominali o superiori
• che i due set di "misure" siano fra loro indipendenti
• che siano noti i valori della probabilita' attesa per i due set di misure
• che si possa inequivocabilmente costruire un test delle ipotesi con una H₀ giustificabile

  The χ² goodness of fit test check whether or not an observed frequency distribution differs from a theoretical distribution. Il χ² test ci permette di studiare se la probabilita' attesa e quella osservata differiscono fra loro per una serie di misure. Questa volta un data set nuovo che e' stato ottenuto con tanta fatica.

  Questo e' uno dei due chi-quadro test cosi' detto goodness of fit e' usato per stimare se le frequenze di una distribuzione osservata differiscono dalle frequenze teoriche (attese) per quell'esperimento. Il test e' normalmente definito con la sigla χ², da non confondere con la distribuzione chi-quadro. Il test e' utile perche' una volta dimostrata la H₀ ci permette di utilizzare i valori ottenuti con quel campionamento per ulteriori studi.

Definizioni:

• la null-hypothesis e' che non ci sia differenza fra le frequenze attese ed osservate, [stated H₀ for f_obs=f_exp]
• dato che studiamo una differenza, al quadrato, usiamo solo il lato maggiore della distribuzione chi-quadro e percio' il test ad una coda, facendo attenzione al calcolo dei gradi di liberta',
• dovendo confrontare una distibuzione reale con una attesa non esiste la condizione di indipendenza, le scale devono essere ad intervallo (opp. a rapporti),
• per chi-quadro e' ancora piu' stringente il numero delle misure, almeno 5 o 7 misure per ogni classe (m, gruppo) ed un totale di almeno 30 o meglio 100 per il totale (n, misure),
• ... un altra null-hypothesis potrebbe essere f_obs > f_exp oppure f_obs < f_exp nei quali casi si puo' usare il test ad una coda.

Calcoli:

  Prendiamo la prima serie di lanci, 501, e chiediamoci se il dado e' truccato oppure no. Avendo da 77 a 91 uscite per ogni classe, ed un totale di 501, possiamo utilizzare il chi-quadro. Se ne avessimo fra 30 e 100 misure dovremmo utilizzare un fattore correttivo (F. Yates).

  Come al solito, graficare le due distribuzioni, quella attesa in blu e quella misurata in verde. Avendo ormai imparato ad utilizzare i grafici puntiamo ad evidenziare le differenze!

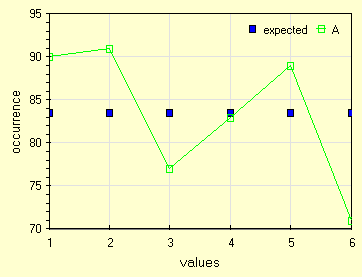le due distribuzioni attesa e rilevata per studiare χ2

  Chi-quadrato e' complesso da capire e da applicare. Qui sopra vediamo un tipico problema, le osservazioni di una qualsiasi classe sono numero interi (quante volte e' uscito il 4) quando le probabilita' sono frazioni e spesso numeri irrazionali. Per piccoli campioni serviranno delle correzioni e per piccolissimi campioni non si puo' piu' utilizzare.

  Almeno questa volta la formula e' chiara:

chi-quadro test formula

  Che nel caso delle due distribuzioni di 6 classi:

• f_i^exp e' il valore proporzionale atteso per ogni classe (83.5 per ogni faccia del dado)
• f_i^obs e' il valore osservato per ogni classe (90 per la faccia 1)
• gradi di liberta, m-1=5
• χ₅² e' uguale a: 3.92215568862276

  Le tavole dei valori critici costruite da Pearson e riportate in forma ridotta da Fisher sono di solito costruite per tutti i valori di probabilita' da 0.005, 0.01, 0.025, 0.05 fino a valori di 0.995. Queste tabelle sono tutte one-side, questo per la particolare forma della distribuzione χ².

  Percio' in questo caso accettiamo un errore di tipo I pari al 5% (cioe' una α=0.05), cioe' una probabilita' per H₀ pari al 95%. Copiamo le opportune tabelle α da un un buon libro.

  Se abbiamo scelto una α pari a 0.05 il valore tabulato 11.071 e' maggiore di quello ottenuto 3.922 percio' l'ipotesi nulla e' accettata. Percio' con una probabilita' del 95% le variazioni osservate sono solo da attribuire al caso.

  Se il numero totale di misure (n) e' compreso fra 30 e 100, ma ogni libro di statistica da valori diversi, e comunque ogni occorrenza di classe (m) e' almeno superiore a 5 o 7, il calcolo di chi-quadro ha bisogno di una delle correzioni di F. Yates.

  Ci sono due correzioni di Yates che cerchiamo di riportare qui:

1. per valori di n molto superiori a 30 e prossimi a 100: si calcolano i valori assoluti delle differenze f_i^exp-f_i^obs; poi alla differenza maggiore si sottrae 0.5 prima di calcolare il quadrato (la faccia 6 nel nostro caso); si cerca poi la differenza minore ed a questa si somma 0.5 prima di calcolare il quadrato (la faccia 4 nel nostro caso). Si calcola chi-quadro come gia' visto;
2. invece per valori di n poco superiori a 30, con i soliti limiti su m, si sottrae 0.5 per ogni valore assoluto delle differenze f_i^exp-f_i^obs e poi si calcola il quadrato, il quoziente, la sommatoria, chi-quadro.

  Sbagliando, visto che non c'e' ne' bisogno, applichiamo le due correzioni all'esempio precedente:

1. ((83.5-90)²/83.5)+((83.5-91)²/83.5)+((83.5-77)²/83.5)+((|83.5-83|+0.5)²/83.5)+((83.5-89)²/83.5)+((|83.5-71|-0.5)²/83.5)=3.78443
2. ((|83.5-90|-0.5)²/83.5)+((|83.5-91|-0.5)²/83.5)+((|83.5-77|-0.5)²/83.5)+((|83.5-83|-0.5)²/83.5)+((|83.5-89|-0.5)²/83.5)+((|83.5-71|-0.5)²/83.5)=3.47305

  Cioe' la correzione di Yates fornisce valori piu' conservativi, e' cioe' piu' difficile rifiutare la H₀ (la correzione si basa sul fatto che diminuendo n e' piu difficile descrivere una popolazione, cioe' con 12 lanci di un dado non bisogna aspettarci di veder uscire due volte ogni faccia!)

  On-line calculator?? Ma non avete un foglio elettronico che almeno non sbagli a fare le differenze ed i quadrati?. Attenzione al calcolo del modulo e delle somme. Buon lavoro.