Fisher F-test, varianza di due distribuzioni

  Fino ad ora praticamente tutti i test erano legati la valore centrale di una distribuzione, nelle sua varie forme, e su questo basavano le ipotesi, magari tenendo conto anche dello spread.

  R.A. Fisher invece in gran parte dei suoi studi di statistica si interessa della varianza, cioe' della forma e della dispersione di una distribuzione. E' un grande passo avanti che ci permettera' la nascita di altri test non solo fra due variabili ma anche multivariati.

  Dato che anche se basato sulle varianze anzi per essere precisi sugli scarti quadratici medi dei campioni si tratta pur sempre di un test parametrico con alcune premesse per la sua validita'.

• che le due distribuzioni siano normali, o almeno che la popolazione da cui si campiona lo sia
• che i singoli campioni siano estratti casulamente dalla popolazione
• che i due set di "misure" siano fra loro indipendenti
• che la scarto quadratico medio S sia una stima di σ
• che si possa inequivocabilmente costruire un test delle ipotesi con una H₀ giustificabile

  The F-test is used to test if the standard deviations of two populations are equal. Definiamo due distribuzioni, anche di numerosita' poco diversa, che provengono dal campionamento di una popolazione. Come nell'esempio seguente che abbiamo gia' usato per un non-parametrico.

  Questo F-test cosi' detto in onore a R.A. Fisher e' usato per confrontare due varianze σ_a e σ_b mediante due loro stime S_a et S_b. Il test e' normalmente definito con la sigla F_(a,b). Il test e' utile perche' una volta dimostrata la H₀ ci permette di stimare σ_a conoscendo S_a.

Definizioni:

• la null-hypothesis e' che le due varianze siano uguali, cioe' σ_a=σ_b, [stated H₀ for σ_a=σ_b]
• di conseguenza si usa il test a due code, visto che la negazione puo' essere positiva o negativa,
• e' richiesto che le misure siano indipendenti, che le scale siano almeno ad intervallo (opp. a rapporti),
• come tutti i test parametrici ci vuole un discreto numero di misure per stimare i parametri della distribuzione. Non e' necessario, seppur auspicabile, che le due numerosita' siano uguali,
• ... un altra null-hypothesis potrebbe essere σ_a > σ_b oppure σ_a < σ_b nei quali casi si puo' usare il test ad una coda.

Calcoli:

  Vista la delicattezza intrinseca dei test parametrici e meglio, come al solito, graficare le due distribuzioni. Usiamo un ampiezza di classe pari a due volte la risoluzione, 0.02 mm. Notiamo che una volta riportate in grafico le due distribuzioni si presentano davvero difficili, altro che mediana e average, queste sono indefinite e' non potrebbero essere usate in un test parametrico.

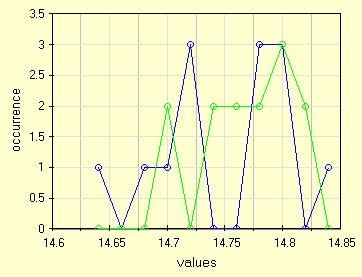le due distribuzioni per il test di Fisher sulle varianze

  Anche se qualche volta c'e' qualche confusione sulla notazione, la formula e' chiara. Ricordiamo che le due varianze vanno poste con S²_a > S²_b, cosi' facendo si avra' sempre F_(a,b) > 1.

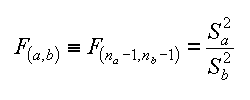F-test, variance ratio

  Che nel caso delle due distribuzioni da 13 misure:

• S²_a e' uguale a, 0.00327564102564103
• gradi di liberta di a, 13-1=12
• S²_b e' uguale a, 0.00162692307692307
• gradi di liberta di b, 13-1=12
• il valore di F, 2.01339637509851

  Le tavole dei valori critici di Fisher sono di solito costruite per valori di probabilita' del 90%, 95% et 99%. Inoltre queste tabelle sono tutte one-side, questo per la particolare forma della distribuzione F. Percio' usiamo una tabella one-side per confermare una H₀ per σ_a=σ_b che sembrerebbe aver bisogno di tabelle double-side, risultato ... usiamo per il test la tabella α/2. Ma questo, a parte una spiegazione a lezione, esula un po dal nostro insegnamento.

  Percio' in questo caso accettiamo un errore di tipo I pari al 10% ed al 2%, cioe' una probabilita' per H₀ pari al 90% ed al 98% (che indica anche una α=0.1 et α=0.02). Copiamo le opportune tabelle α/2 da un un buon libro.

  Avendo scelto una probabilita' del 90% (ricordiamoci α/2) il valore tabulato 2.687 e' maggiore di quello ottenuto 2.013 percio' l'ipotesi nulla e' accettata.

  Se abbiamo scelto una probabilita' del 98% (ricordiamoci α/2) il valore tabulato 4.155 e' anchesso maggiore di quello ottenuto 2.013 percio' l'ipotesi nulla e' accettata.

  In questo esempio si vede ancora meglio il funzionamento della matrice 2x2 legata alle ipotesti H₀ ed H₁. Se accettiamo di commettere un errore di tipo 1 (cioe' che H₀ e' vera ma noi la rifiutiamo) con un α=0.02 il valore di F_(a,b) deve essere molto grande; la nostra forte preoccupazione di non commettere errori del I tipo ci fa accettare valori di F_(a,b) molto grandi fino a 4.155. Forse per questo, ma non solo, il test piu' usato e' quello con α=0.05, il 95%.

  Prima una precisazione: sono state lasciate tutte le cifre decimali prodotte dai calcoli per permettere il confronto con altri software, chiaramente se questi numeri comparissero in una pubblicazione e/o relazione sarebbero sbagliati.

1. i seguenti calcolatori on-line NON sono stati provati uno ad uno per la loro correttezza, come neache tutti i testi sono stati letti, attenzione, attenzione,
2. F-test, tables, NIST americano, tre tabelle per F test, one-sided, con tanti gdf, ricordiamo che la riga e' per S_a, quello maggiore, e la colonna per S_b

  The F-test can be also used to estimate how many measures are necessary to obtain a stated α. Cioe' possiamo chiederci, "definita una probabilita' α, quanti dati servono affinche l'ipotesi nulla possa essere accettata o respinta con una probabilita' β di comettere errori di tipo II?".

  Le formule non sono dovute a Fisher ma utilizzano la sua distribuzione e quella di Gauss per stimare un numero minimo di misure. Una delle formule:

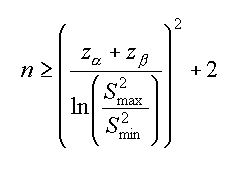Raghavarao estimation of nmin

  In cui, con i soliti parametri:

• S²_max e' la varianza con valore maggiore (chiamata anche S²_a)
• S²_min e' la varianza con valore minore fra le due (chiamata anche S²_b)
• ln e' il logaritmo naturale (in base e)
• z_α e' il valore della distribuzione normale per la probabilita' α
• z_β e' il valore della distribuzione normale per la probabilita' β
• n e' il numero minimo di coppie di dati necessari

  Lo stimare quanti dati saranno necessari per il nostro test e' detto dagli statistici stimare la "Potenza a Priori". Parametro necessario ma che implica delle assunzioni sugli errori del I e del II tipo, anzi sul loro legame come si vede dal numeratore delle formula, che spesso sono difficili o aleatorie.

  Sulla formula e sul concetto qui espresso ci sarebbe da dire tanto, e' una tautologia, per "stimare" devo gia' conoscere S_a et S_b cioe' ha gia' svolto le misure su di un umero n di oggetti. Allora la formula ci dice se il numero n usato e' sufficiente se avessimo scelto richeisto un valore di α e β. Questo giusto per far capire le implicazioni che ci sono dietro una formula ed una scelta.

  Sui testi di statistica si trovano varie formule che esula dal nostro contesto. Per pochi campioni, cioe' nella numerosita' prevista da Gosset si puo' usare una criterio per diminuire la soggettivita' nella scelta di α e β, legandoli fra loro con la formula.

1-β = 1-4α

  Magari dopo aver riletto la slide su H₀ ed H₁ e su "errore di tipo I" ed "errore di tipo II" e "costo dell'errore" possiamo esplicitare i casi piu' frequenti:

α=0.01 e β=0.05 oppure α=0.02 e β=0.10 ed anche α=0.05 e β=0.20

I valori di Z li trovate in tante tabelle e ne abbiamo parlato anche in una slide (z che sottende il 95% dei dati