Gosset's t-test, four of five tests

  ... Little experience is sufficient to show that the traditional machinery of statistical processes is wholly unsuited to the needs of practical research. Not only does it take a cannon to shoot a sparrow, but it misses the sparrow! The elaborate mechanism built on the theory of infinitely large samples is not accurate enough for simple laboratory data. Only by systematically tackling small sample problems on their merits does it seem possible to apply accurate tests to practical data. Such at least has been the aim of this book. (Sir Ronald Aylmer Fisher, 1925/34, preface of "Statistical Methods for Research Workers", 978-0198522294)

  Ma scopo del corso NON e' spiegare il testo di W.S. Gosset (non essendo noi R.A.Fisher puo' essere tanto difficile spiegare quanto facile sbagliare!) ma descrivere qualche applicazione del test di Student che tanto si trova citato e qualche volta a sproposito. Ma per far questo e' nata una delle silde piu' lunghe!

  Abbiamo invece capito che i test non-parametrici gia' visti, il campionamento statistico, qualche misura in meno ma con piu' qualita', ci permettono/impongono nei settori dei Beni Culturali e nell'Ambiente "samples", cioe' piccoli numeri da trattare con attenzione per essere Pertinenti e Rappresentativi.

  Dato che di t-test ce ne sono almeno 4 (anzi forse 5) e per capire come usarli si possono leggere 9 libri senza risolvere nulla (ma forse basta leggere 978-0942154917 et 978-0942154993). Meglio iniziare con una descrizione delle condizioni necessarie affinche' questo ed altri test parametrici abbiano validita':

• che la distribuzione della popolazione sia normale
• che i singoli campioni sia estratti casulamente dalla popolazione
• che le "misure" siano fra loro indipendenti
• che la media X soprasegnato (X bar) sia una stima della media μ
• che la scarto quadratico medio S sia una stima di σ
• che si possa inequivocabilmente costruire un test delle ipotesi con una H₀ giustificabile

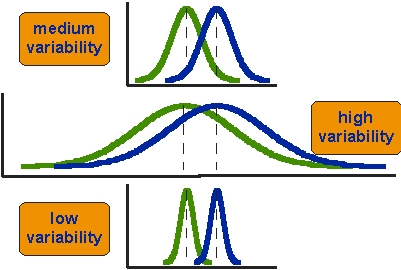
  Tutti i t-test hanno la struttura di un rapporto [ratio structure], cioe' sono una misura del rapporto segnale/rumore [signal/noise ratio]. Il numeratore e' la differenza fra due medie, fra una misura e la media o similare, cioe' la differenza fra due segnali reali e misurabili; il denominatore misura la variabilita', cioe' la dispersione, cioe' il rumore che la casualita' inserisce nella/nelle misure. Una immagine di esempio, stessa differenza fra i segnali ma ben diverso e' il rumore.

from: http://www.socialresearchmethods.net/kb/stat_t.php

  Visti nell'ottica S/N ratio tutti i test si semplificano, bisogna solo trovare cosa mettere sopra e sotto la linea di frazione e decidere quanto "rumore" accettare. Nel secondo caso delle figura qui sopra non saremo mai sicuri della reale differenza fra le due distribuzioni; nel terzo caso invece il t-test dovrebbe mostrarci la loro diversita'.

  Test whether the mean of one variable differs from a constant. Dato un campionamento con n oggetti di una popolazione, con le solite limitazioni viste prima, possiamo calcolare la varianza del campione, il suo S, la sua media X soprasegnato (X bar).

  Della popolazione potremmo aver misurato con qualche altro metodo la media μ, ed invece cerchiamo la media attesa che dovremmo prevedere dal campionamento detta μ₀. Come al solito possiamo usare uno dei campionamenti delle provette.

  A quanto sembra il random start era' 4.

  Questo t-test di Gosset e' quello per confrontare una media osservata con una media attesa. Il test e' normalmente definito con la sigla t_(n-1). Il vero t-test confronterebbe la media campionaria con la media della popolazione ma spesso quest'ultima e' incognita.

Definizioni:

• la null-hypothesis e' che la media μ (popolazione) e' uguale a quella attesa μ₀ (prevedibile da tanti campionamenti), [stated H₀ for μ=μ₀]
• di conseguenza si usa il test a due code, visto che la negazione puo' essere positiva o negativa,
• e' richiesto che le misure siano indipendenti, che le scale siano almeno ad intervallo (opp. a rapporti),
• come tutti i test parametrici ci vuole un discreto numero di misure per stimare i parametri della distribuzione. Di solito si usa un numero totale compreso fra una decina e la soglia di Student,
• il calcolo del valore μ₀ e' difficile dovendo provenire da piu campionamenti, (difficile sia come formulazione che come esecuzione),
• l'assenza di misure replicate e' auspicabile, cioe' i diversi campionamenti per la stima di μ₀ non dovrebbero avere oggetti in comune (ma stesso strumento, stesso operatore, misure consecutive, stesse condizioni al contorno),
• ... un altra null-hypothesis potrebbe essere μ > μ₀, in ambo i sensi, in quel caso si puo' usare il test ad una coda.

Calcoli:

  Riaffermando che i test parametrici sono "delicati" e basta una svista per inficare un risultato, come al solito prima grafichiamo la distribuzione, visto che abbiamo un numero sufficiente di valori per formare delle classi. Usiamo un ampiezza di classe pari a due volte la risoluzione, 0.02 mm.

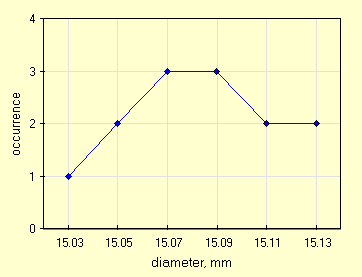distribuzione per classi, 13 dati

  Per mezzo di 4 campionamenti otteniamo una μ₀=15.09 (dovuta a disegni differenti, ma con qualche ripetizione).

  Di formule se ne trovano tante, complesse, semplici, palesemente sbagliate, questa speriamo sia quella giusta.

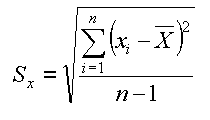la media campionaria verso l'attesa	formula di Sx

  In cui, nel caso dei 13 diametri delle provette sotto il tappo:

• n_A per il numero di oggetti, 13,
• X soprasegnato per la media del campione, 15.0792307692308
• S_x e' lo scarto quadratico medio del campione, 0.0292863843396946
• μ e' il valore della media attesa 15.09
• t_(n-1) e' il valore di t da confrontare con le tabelle, -1.326

  Come al solito facciamo due test con probabilita' al 80% ed al 95% (cioe' α=0.2 et α=0.05). Copiamo una tabella da un buon libro.

  Se abbiamo scelto una probabilita' del 80% il valore tabulato 1.356 e' maggiore di quello ottenuto 1.326 (preso come modulo) percio' l'ipotesi nulla e' accettata.

  Se abbiamo scelto una probabilita' del 95% il valore tabulato 2.179 e' maggiore di quello ottenuto 1.326 percio' l'ipotesi nulla e' accettata. Cioe' possiamo scrivere: -2.179 < t < 2.179 visto che usiamo un test a due code.

  Ricordiamo che: a) della nostra esercitazione usiamo i diametri misurati sotto il tappo che sappiamo essere quasi una gaussiana, b) sulla definizione di media attesa ci sono cento definizioni!

  Often are used to compare the means of two independently sampled groups. Utile per compare le medie di due distribuzioni ottenute dal campionamento di una sola popolazione. Questo sarebbe uno dei veri t-test, qualche volta e' anche utilizzato per comparare: due gruppi di pazienti con due diversi trattamenti; due misure di durata di una serie di lampadine, ma distorcendo il test.

  Veramente di questi ce ne sarebbero tre, questi di seguito, ma se scriviamo la formula dell'ultimo, il c), questa dovrebbe andar bene anche per i primi due, magari semplificandola.

1. equal sample sizes, equal variance;
2. unequal sample sizes, equal variance;
3. unequal sample sizes, unequal variance.

  Questa volta e' ancora piu' importante definire il t-test di Gosset, quello per confermare che due medie campionarie provengono dalla stessa popolazione. Il test e' normalmente definito con la sigla t_(n1-n2). Oppure definito come t_(n1+n2-2). Ma quella del punto c) e' anche definito come t ⁱ.

Definizioni:

• la null-hypothesis e' che la media μ_A e' uguale a quella μ_B prevenendo tutte e due dalla media μ della popolazione, [stated H₀ for μ_A=μ_B]
• il test confronta i due valori X_A soprasegnato ed X_B soprasegnato (X_B bar) che sono le medie campionarie, le uniche veramente disponibili,
• di conseguenza si usa il test a due code, visto che la negazione puo' essere positiva o negativa,
• e' richiesto che i due campionamenti siano indipendenti, che le scale siano almeno ad intervallo (opp. a rapporti),
• come tutti i test parametrici ci vuole un discreto numero di misure per stimare i parametri delle due distribuzioni. Non e' necessario che n_A sia uguale ad n_B ma e' auspicabile,
• l'assenza di misure replicate e' auspicabile, cioe' i diversi campionamenti per la stima di X_A soprasegnato et X_B soprasegnato non dovrebbero avere oggetti in comune,
• ... un altra null-hypothesis potrebbe essere X_A > X_B, in ambo i sensi, in quel caso si puo' usare il test ad una coda.

Calcoli:

  Date due distribuzioni una rappresentazione grafica gia' da sola puo' aiutare a comprendere la similarita', anche se non puo' misurarla. Usiamo anche questa volta una ampiezza di classe pari a 0.20 mm.

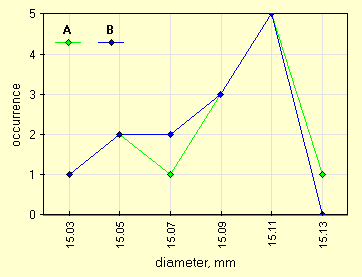le due distribuzioni campionarie, na=13, nb=13

  Il solito problema di trovare le formule giuste, forse queste. Avevamo detto che iniziavamo con unequal sample sizes, unequal variance.

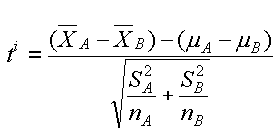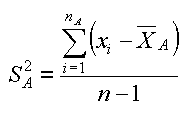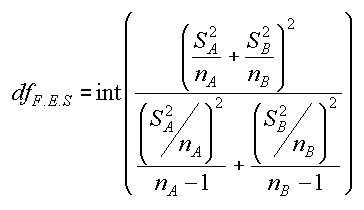t-test, 2 campionam. indip., diff. varianze	solita formula di S2, per SA et SB	degrees of freedom, by F. E. Satterthwaite, 1946

  La formula per il calcolo dei gradi di liberta' non e' la solita n-1 ma una formula di approssimazione di F.E. Satterthwaite (An Approximate Distribution of Estimates of Variance Components, Biometrics Bulletin, 2(6), 1946, 110-114).

  Nella formula del calcolo di tⁱ l'espressione (μ_A-μ_B) e' uguale a zero vista l'ipotesi H₀. Questo e' un ragionamento sottile, se confermeremo H₀ abbiamo fatto bene ad annullarla, se non la confermeremo non potevamo cancellare questa differenza.

  Da cui, nel caso delle 13+13 misure dei diametri delle provette:

• n_a per il numero di oggetti, 13, cosi' come n_b
• X_A soprasegnato per la media del campione A, 15.0823076923077
• X_B soprasegnato per la media del campione B, 15.0792307692308
• S²_A e' la varianza del campione A, 0.000802564102564096
• S²_B e' la varianza del campione B, 0.000724358974358961
• con la formula di destra per df_FES otteniamo il valore 23
• tⁱ e' il valore di t da confrontare con le tabelle, 0.283909376395268

  Vista la piccola differenza fra le varianze avremmo potuto anche usare una formula riodotta per unequal sample sizes, equal variance.

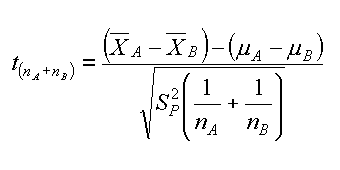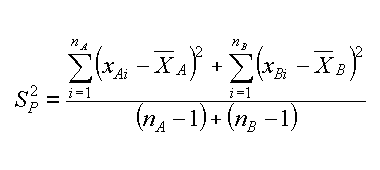t-test, 2 campionam. indip., uguali varianze	formula di S2, pooled

  Queste due formule danno un risultato molto simile per il test, ma i gradi di liberta' questa volta sarebbero df=(n_A-1)+(n_B-1)=24, uno in piu' di quelli calcolati con la formula precedente. Come al solito facciamo due test con probabilita' al 80% ed al 95% (cioe' α=0.2 et α=0.05). Copiamo una tabella da un buon libro.

  Se abbiamo scelto una probabilita' del 80% il valore tabulato 1.319 e' maggiore di quello ottenuto 0.284 percio' l'ipotesi nulla e' accettata.

  Con una probabilita' del 95% il valore tabulato 2.069 e' maggiore di quello ottenuto 0.284 percio' l'ipotesi nulla e' accettata. Cioe' possiamo scrivere: -2.069 < tⁱ < 2.069 visto che usiamo un test a due code.

  Anche usando la formula approssimata e 24 df si avrebbe lo stesso risultato stando cosi' lontani dai valori di soglia.

  Used to compare means where the two groups are correlated, as in before-after, repeated measures, matched-pairs, or case-control studies. Usato quando le due distribuzioni sono correlate. In questo esempio prima del campionamento 11 provette sono state misurate dai 3 gruppi di lavoro proprio per vedere se c'e' qualche differenza significativa fra i gruppi. Cioe' studiamo cosa si ottiene usando lo stesso strumento/oggetti ma un diverso operatore inserito in un diverso contesto lavorativo.

  Anche di questo t-test ce ne sarebbero due, questi: a) compariamo la ripetizione delle misure su n oggetti e NON ci aspettiamo una differenza b) ci aspettiamo che una qualche modifica sugli oggetti ABBIA prodotto una differenza pari a δ.

  Sembrano la stessa cosa ma dietro questa sottile differenza ci sono miliardi di euro di eventuali profitti da parte di qualche casa produttrice di XYZ, migliore di YXZ.

  Come al solito a questo punto la definizione del t-test di Gosset, questo e' per confrontare le differenze fra le misure appaiate ripetute sugli STESSI oggetti. Il test e' normalmente definito con la sigla t_d. Oppure definito come t_δ.

Definizioni:

• la null-hypothesis e' che la differenza media fra le misure, D soprasegnato, sia zero, [stated H₀ for Dbar=0]
• il test confronta i due valori ottenuti per LO STESSO oggetto campionario, calcola D_a-b, calcola D soprasegnato (D bar),
• di conseguenza si usa il test a due code, visto che la negazione puo' essere positiva o negativa,
• e' richiesto che i due campionamenti siano indipendenti nel tempo ma applicati allo stesso oggetto, che le scale siano almeno ad intervallo (opp. a rapporti),
• come tutti i test parametrici ci vuole un discreto numero di misure per stimare se veramente c'e' o non c'e' una differenza media,
• dato che questo t-test e' anche una misura dell'intervento del tempo necessita che "lo strumento" di misura ne sia immune,
• ... un altra null-hypothesis potrebbe essere D soprasegnato = δ, cioe' che la differenza media micurata e' uguale ad una da noi attesa detta δ.

Calcoli:

  Questa volta i grafici possibili sono due, quello classico con la distribuzione per classi (dopo una attenta scelta dell'ampiezza di classe), l'altro e' il Ladder Graph che puo' essere usato anche nel Wilcoxon Matched-Pairs Test che abbiamo gia' visto.

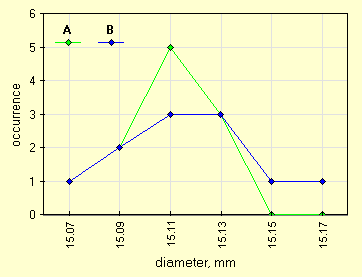11 dati appaiati, due diversi operatori

  Uno dei grafici poco usati ma molto potenti per conforntare dei dati appaiati e' il Ladder Graph che con qualche trucco si puo' ottenere anche da uno spreadsheet. L'asse Y mostra i valori misurati. L'asse X mostra il tempo anche se con soli due punti, quello iniziale e quello finale. Ogni punto ha una retta che collega i due valori iniziale e finale. Quello qui sotto evidenzia con due colori i tratti ascendenti e discendenti.

  Ladder Graph e' utile quando ci sono pochi oggetti da mostrare, una decina o poco piu'. Si nota anche l'ampiezza e il raggruppamento delle due distribuzioni sull'asse Y, delle misure.

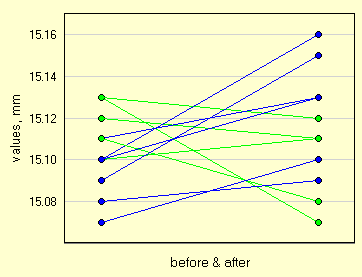Ladder Graph per 11 dati appaiati

  Questa volta sulle formule non c'e confusione. Anzi ripetiamo il calcolo di S² che va calcolato sulle differenze.

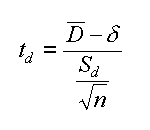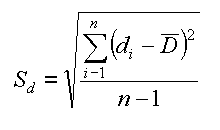t-test, 2 camp. dipend.	formula di Sd (sulle differenze)

  Lo scarto quadratico e' calcolato sulle differenze. Qualche parola bisogna spenderla sul valore di δ che puo' essere:

• δ=valore noto, per una differenza che dovrebbero' presentare magari dopo un trattamento (peso di n campioni di intonaco posti in stufa);
• δ=0, per casi come quello dell'esempio in cui NON ci deve essere differenza fra operatori che usano lo stesso strumento
• S_d e' lo scarto quadratico medio delle differenze, 0.0363318042491702
• t_d e' il valore di t da confrontare con le tabelle, -0.912870929175279

  Visto che trattasi di una esercitazione di laboratorio non siamo troppo stringenti con le probabilita', testiamo al 80% ed al 95% (cioe' α=0.2 et α=0.05). Copiamo una tabella da un buon libro.

  Se abbiamo scelto una probabilita' del 80% il valore tabulato 1.363 e' maggiore di quello ottenuto 0.913 (preso come modulo) percio' l'ipotesi nulla e' accettata.

  Se abbiamo scelto una probabilita' del 95% il valore tabulato 2.201 e' maggiore di quello ottenuto 0.913 percio' l'ipotesi nulla e' accettata. Cioe' possiamo scrivere: -2.201 < t_d < 2.201 visto che usiamo un test a due code. Cioe' non si rilevano differenze fra i due operatori che hanno svolto le misure.

  Nelle misure spesso ci si trova di fronte ad un valore che non sembra far parte della distribuzione. La domanda che ci si pone e' se trattare questo dato come un outlier. Quando si sta eseguendo un campionamento, con un piccolo numero (<30 ?) di "oggetti" estratti da una popolazione finita e misurabile si puo' usare uno dei test di Gosset.

  Questo non sostituisce uno dei vari test per la ricerca di outlier(s) ma si affianca ad essi. Questo test ci conferma se il valore fa parte della popolazione (oppure al contrario se fa parte di un altra popolazione).

  Il "with replacement" NON e' avvenuto, per cui non ci sono replicati (una prima condizione del test!).

  Uno dei t-test di Gosset e' quello per verificare se l'oggetto, la sua misura, fa parte della popolazione rispetto agli oggetti, le loro misure, gia' campionati. Il test e' normalmente definito con la sigla t_(na-1).

Definizioni:

• la null-hypothesis e' che la misura non fa parte della distribuzione campionaria,
• di conseguenza si usa il test a due code, visto che il dato non deve cadere all'interno della distribuzione di probabilita',
• e' richiesto che le misure siano indipendenti, che le scale siano almeno ad intervallo (opp. a rapporti),
• come tutti i test parametrici ci vuole un discreto numero di misure per stimare i parametri della distribuzione. Di solito si usa un numero totale compreso fra una decina e la soglia di Student,
• e' richiesto che la popolazione abbia una distribuzione Gaussiana (anche se il t-test sopporta una piccola deviazione),
• l'assenza di misure replicate e' necessaria, il valore sotto indagine deve provenire da una misura indipendente con tutte le fonti di disturbo uguali (stesso strumento, stesso operatore, misure consecutive, stesse condizioni al contorno) per cui l'unica variazione e dovuta all'oggetto stesso,
• ... un altra null-hypothesis potrebbe essere che il valore non fa parte della distribuzione campionaria, per eccesso o per difetto, in quel caso si puo' usare il test ad una coda.

Calcoli:

  Riaffermando che i test parametrici sono "delicati" e basta una svista per inficare un risultato, come al solito prima grafichiamo la distribuzione, visto che abbiamo un numero sufficiente di valori per formare delle classi. Usiamo un ampiezza di classe pari a due volte la risoluzione, 0.02 mm.

distribuzione per classi, 13 dati

  La null-hypothesis e' che il valore 15.07 non faccia parte della distribuzione. Usiamo il t-test di Student/Gosset per confronto fra una osservazione e la media di un campionamento.

  Di formule se ne trovano tante, complesse, semplici, palesemente sbagliate, questa e' quella giusta (speriamo).

una misura e' parte della distribuzione?	formula completa per uno spreadsheet

  In cui, nel caso dei 13 diametri delle provette:

• n_A per il numero di oggetti, 13,
• x_A soprasegnato per la media del campione, 15.1107692307692
• S²_A e' la varianza del campione, 0.000674358974358986
• x_j e' il valore sotto esame, 15.07
• t_(nA-1) e' il valore di t da confrontare con le tabelle, -1.513

  Come al solito facciamo due test con probabilita' al 80% ed al 95% (cioe' α=0.2 et α=0.05). Copiamo una tabella da un buon libro.

  Se abbiamo scelto una probabilita' del 80% il valore tabulato 1.356 e' minore di quello ottenuto 1.513 percio' l'ipotesi nulla e' rigettata.

  Se abbiamo scelto una probabilita' del 95% il valore tabulato 2.179 e' maggiore di quello ottenuto 1.513 percio' l'ipotesi nulla e' accettata. Cioe' possiamo scrivere: -2.179 < t < 2.179 visto che usiamo un test a due code.

  Forse sarebbe piu' corretto usare una qualche tecnica di cross-validation in cui l'oggetto sotto esame non prende parte alla costruzione del modello, ne riparleremo a lezione.

  Just measured Pearson's r really measure a correlation or a chance? Appena dopo aver calcolato un coefficiente di correlazione fra due variabili ci si deve chiedere se questo e' significativo o e' solo dovuto al caso.

  Prendiamo il data set cosidetto "scarpeshoes", nella sua prima versione che conteneva solo 14 misure e vediamo se la correlazione ottenibile e' significativa (r=0.88056484952946).

  Questa volta il t-test di Gosset serve per verificare che il cofficiente di correlazione r non sia dovuto al caso ma sia significativo tenendo conto del numero di misure, senza replicati. Il test e' normalmente definito con la sigla t_(r).

Definizioni:

• la null-hypothesis e' che, nonostante sia misurabile una r sulla popolazione, la correlazione nella popolazione ρ sia uguale a zero, [stated H₀ for ρ=0],
• di conseguenza si usa il test a due code, visto che la correlazione puo' allontanarsi dallo zero in ambedue i sensi,
• e' richiesto che gli errori associati siano omoscedastici ed indipendenti fra X ed Y, che le scale siano almeno ad intervallo (opp. a rapporti),
• per il calcolo di r servono un discreto numero di misure, anzi il test e' molto legato al valore di n,
• e' richiesto che la popolazione abbia una distribuzione Gaussiana (come si vedra' meglio da un paio di grafici qui sotto),
• l'assenza di misure replicate e' necessaria, la coppia di valori che formano r devono provenire da misure indipendenti con tutte le condizioni al controno uguali,

  Rileggendo quanto qui sopra scritto noi imponiamo che NON ci sia correlazione nella popolazione ed attraverso il t-test ci facciamo smentire. Ma un altra null-hypothesis potrebbe essere che ρ=m, cioe' uguale ad un valore noto per la popolazione. Questo e' molto poco usato e la sua formulazione e realizzazione esula dallo scopo di queste slide.

Calcoli:

  Come sempre prima qualche grafico e poi le formule da applicare. Questa volta necessita che dal bel libro on-line del Prof. L. Soliani di Parma rubiamo due disegni.

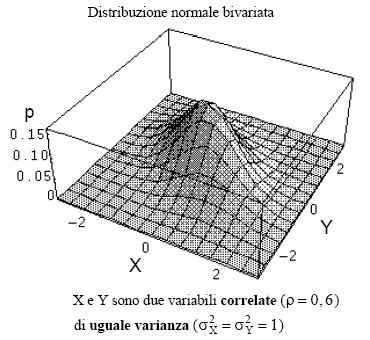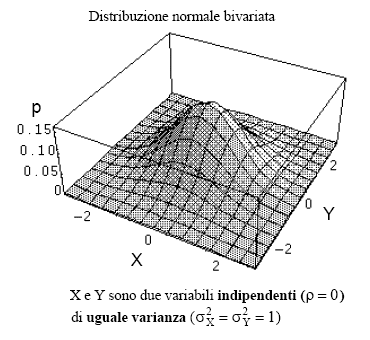
doppia distribuzione gaussiana su X e su Y	ma in questo caso c'e' anche una correlazione

  Quella mostrata e' la popolazione delle X e delle Y che a sinistra mostra solo un picco di probabilita'. A destra invece la struttura e' diversa, la "montagna" si pone sulla diagonale del piano XY, si nota una correlazione. Ora come al solito grafichiamo i nostri dati.

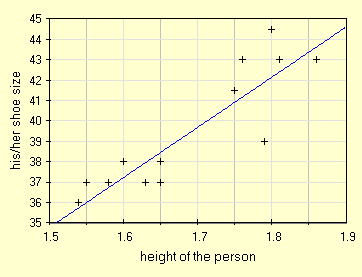con soli 14 valori sembra presente un correlazione lineare

  La formula e' gia' stata presentata precedentemente. E' appena il caso di ricordare che n-2 e' dovuto a due vincoli la variabile indipendente e la pendenza.

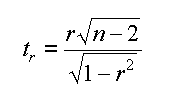significance of r

  In cui, nel caso delle 14 persone campionate:

• n_A per il numero di oggetti, le persone 14,
• r il coefficiente di correlazione, 0.88056484952946
• t_r e' il valore di t da confrontare con le tabelle, 6.436

  Come al solito facciamo due test con probabilita' al 80% ed al 95% (cioe' α=0.2 et α=0.05). Copiamo una tabella da un buon libro.

  Avendo scelto una probabilita' del 80% il valore tabulato 1.356 e' minore di quello ottenuto 6.436 percio' l'ipotesi nulla e' rigettata.

  Se abbiamo scelto una probabilita' del 95% il valore tabulato 2.179 e' anchesso minore di quello ottenuto 6.436 percio' l'ipotesi nulla e' rigettata. Cioe' non possiamo affermare che ρ=0, il coefficiente r e' significativo.

  Prima una precisazione: sono state lasciate tutte le cifre decimali prodotte dai calcoli per permettere il confronto con altri software, chiaramente se questi numeri comparissero in una pubblicazione e/o relazione sarebbero sbagliati.

  Di calcolatori on-line e di testi se ne trovano tanti, spesso sbagliati, una breve selezione pero' porta a consigliare il libro on-line del Prof. Lamberto Soliani, Universita' di Parma. Inoltre possiamo citare:

1. i seguenti calcolatori on-line NON sono stati provati uno ad uno per la loro correttezza, come neache tutti i testi sono stati letti, attenzione, attenzione,
2. www.statsdirect.com, questo e' l'help generale in cui nell'index dovete cercare i tre t-test,
3. Ying Zhang, una comparazione fra i vari t-test con le formule,
4. graphpad.com/index, l'indice da cui partono una serie di calcolatori on-line, e di spiegazioni,
5. SISA, un altro indice con tanti tanti test on-line e descrizioni dei metodi,
6. Kenneth Janda, alla Northwestern University, la descrizione dei vari t-test sta nelle Testing Hypotheses.