| Rome University, La Sapienza Chemistry Department Rome, Italy, Europe |
Dr. Giovanni Visco Cenni di statistica di base. Calcoli di regressioni e correlazioni. dicembre 2006 |
Corso di Laurea in Scienze Applicate ai Beni Culturali ed alla Diagnostica per la loro Conservazione |
| previous slide, 54 | next slide, 55b |
Questa volta non ci sono ambiguita', il test e' di sicuro parametrico (basandosi sulla varianza) e' datato 1920, introdotto per la prima volta da R.A. Fisher quasi a prosecuzione della sua spiegazione del χ2 test e del t test.
Di test ANalysis Of VAriance ce ne sono vari, fra i principali: One-way ANOVA per testare la differenza nella media fra tre o piu' gruppi di misure; Repeated-measures ANOVA che confronta per esempio l'applicazione di due strumenti sugli stessi oggetti; Factorial ANOVA per analizzare i risultati di un D.O.E. di cui nelle slide c'e' un capitolo a parte; Multivariate-analysis-of-variance MANOVA, che pero' esula da questa slide e' andrebbe inserita nel capitolo chemiometria. Noi qui spiegheremo la prima di queste.
Qualche ipotesi preliminareOne-way ANOVA confronta le varianze fra due o piu' distribuzioni (di solito almeno tre), confronta le frequenze attese e quelle osservate (sperimentali) per attribuire un significato statistico alle medie osservate, con qualche precondizione in piu':
The reason this analysis is called ANOVA rather than multi-group means analysis (or something like that) is because it compares group means by analyzing comparisons of variance estimates. Buona spiegazione. ANOVA ci permette di studiare una serie di campionamenti o una serie di applicazioni di metodi/misure/procedure/strumenti sulla popolazione e vedere se la media ottenuta e' uguale. Dato che necessiteremmo di conoscere la probabilita' attesa perche' non barare un po' e riusare uno dei data-set gia' visti?
| upper side | expected value | gambler n. 1 | gambler n. 2 | gambler n. 3 |
| 1 | 83.50 | 90 | 89 | 97 |
| 2 | 83.50 | 91 | 87 | 82 |
| 3 | 83.50 | 77 | 80 | 76 |
| 4 | 83.50 | 83 | 73 | 85 |
| 5 | 83.50 | 89 | 85 | 86 |
| 6 | 83.50 | 71 | 87 | 75 |
Da cui possiamo definire facilmente l'ipotesi H0 e' cioe':
H0: μ1=μ2=μ3
Copiando si impara? Usiamo invece di questo un data set di un libro (vedi ISBN:0942154916) che spesso consiglio, ben scritto, con i concetti e poche formule. Questo e' il data-set.
| n. sold for | blue package | red package | green package |
| 1st day | 6 | 18 | 7 |
| 2nd day | 14 | 11 | 11 |
| 3rd day | 19 | 20 | 18 |
| 4th day | 17 | 23 | 10 |
| color average | 14.00 | 18.00 | 11.50 |
| variance, s2 | 32.67 | 26.00 | 21.67 |
| overall arith.mean | 14.50 | ||
| overall s2 | 29.73 |
Descriviamo il data-set: una azienda che produce the (oppure tè) decide di sostituire il solito pacchetto grigio con uno colorato, non cambiane ne le scritte, ne la forma, ne il contenuto, solo il colore dominante e' un blu, un rosso, un verde. Il marketing office decide di testare queste nuove scatole in 12 supermercati random chosen dello stesso livello, e per pochi giorni cosi' da vedere l'effetto del colore sul numero di vendite.
Ora che da chemiometri ci siamo avventurati in un campo a noi sconosciuto ci beccheremo tutte le critiche di qualche Prof. di marketing che ci dice che NON si fa cosi' una campagna, ma questo e' un data-set vecchio di 40 anni e cosi' e' descritto.
L'ipotesi H0 e' la stessa di prima, cioe': H0: μb=μr=μg che se fosse rispettata non ci sarebbe un "effetto colore" nelle vendite.
Notate il piccolo numero dei campioni e delle ripetizioni.
Se la ipotesi H0 e' vera allora la differenza fra le medie misurate e' solo dovuta al caso. Ci serve la statistica di Fisher per confermare o rigettare l'ipotesi H0.
Cioe' sigma od esse? Oppure lo scarto della popolazione o del campione?.
Anche se dall'esempio di prima sembra che stiamo lavorando sulla popolazione di tutti i the di nuovo colore effettivamente e' un campione, si potevano scegliere diversi supermercati, allungare il numero di giorni, cambiare i giorni stessi.
Perche' poi si chiami anoVA e non anoRMSQ non lo so ma ricordatevi di usare @vars( ) in Lotus, =var( ) in Excel o in qualsiasi altro software usate.
Per calcolare f ci servono due varianze. Una la troviamo gia' nella tabella qui sopra, cioe' la varianza calcolata per ognuno dei colori. Come ci si aspetterebbe se l'ipotesi H0 fosse vera non c'e' una varianza molto diversa dalle altre, ci tocca calcolare la varianza pool (la formula completa per n. diversi nei gruppi, qui n=4 giorni, e' in una slide precedente), nel nostro caso:
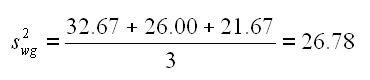
Questa varianza non va confusa con quella calcolata su tutte le misure, in questo caso sulle 174 scatole di the vendute. I valori per l'intera matrice sono:
| matrix sum (items sold in total) | 174 |
| matrix arithmetic mean (avg of items sold in any shop) | 14.50 |
| matrix variance (variance for any shop) | 29.73 |
| matrix median (more accurate estimation of central values) | 15.50 |
Ma questi sarebbero i dati di vendita di quel tipo di te a prescindere dal colore della scatola, di quanto in media (o mediana) vende uno shop per pianificare i rifornimenti mensili, etc.. Ma noi servira il confronto fra i tre gruppi non il totale.
Abbiamo detto che per calcolare f ci servono due varianze. Una l'abbiamo gia' calcolata (sw2 = 26.78), l'altra la estraiamo dalla medie di ogni gruppo,
xb = 14.00 , xr = 18.00 , xg = 11.50 , xt = 14.50
Ora direte che calcolare la varianza su tre numeri e' un po ridicolo, ma se rileggete la definizione dello scarto quadratico medio che qui stiamo cacolando, e' fatto per i piccoli campioni, in via ipotetica si puo' calcolare il RMSD di due soli numeri, cioe' la differenza o lo spread.
La formula e' la solita, lo RMSD rispetto alla media di tutta la matrice, scriviamola:
((14.0-14.5)2 + (18.0-14.5)2 + (11.5-14.5)2) / 2 = 10.75
Ma questa e' la stima della varianza delle media, non la stima della varianza della popolazione. Da qualche parte abbiamo gia' trovato la formula, ma riscriviamola qui:
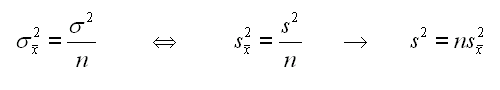
Quella di centro e' quella che ci interessa da cui si ricava quella di sinistra. Data la formula possiamo ora calcolare ed ottenere la seconda varianza che ci serve.
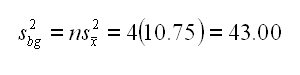
Ricordiamoci che questo sbg2 racchiude sia la varianza tra i gruppi (i supermercati in questo caso) ma anche la variazione dovuta al diverso trattamento (i colori in questo caso).
Ora che abbiamo due indipendenti stime della varianza possiamo calcolare il F di Fischer come rapporto fra le due, la solita formula.
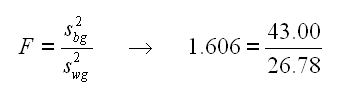
Questo rapporto fra between groups e within groups andra' forse corretto con qualche parametro, ma forse ora e' meglio descrivere meglio i due valori di n=4 et k=3.
Gradi di liberta', ne abbiamo gia' parlato ed ogni volta e' un piccolo problema calcolare quanti sono davvero, almeno per i neofiti della statistica. Qui e' piu' semplice, siamo in un campionamento di una popolazione per cui il termine n-1 e' quello corretto.
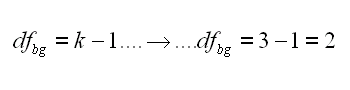
Per peggiorare la comprensione di chi forse aveva capito, data la media dei gruppi 14.5 solo due medie possono variare per ottenere detto valore, la terza e' fissata (pensate ad un triangolo, data la somma dei cateti se ne variate due il terzo deve chiudere il totale ed e' bloccato nel suo valore).
Nel caso within groups invece bisogna tener conto che i gruppi "potrebbero" avere numerosita' differente, la formula e' percio' una sommatoria, questa:
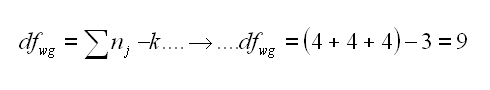
Ed anche qui ogni n di un gruppo ha il suo n-1 per calcolare i gradi di liberta' di quel gruppo, potreste anche cacolare cosi: (4-1)+(4-1)+(4-1)=9 se piu' vi sembra comprensibile.
E finalmente i valori che ci serviranno per la ricerca nella tabelle, storiche, di F. Si scrive per convenzione con la virgola che li separa.
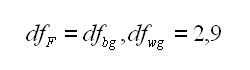
Abbiamo il valore di F=1.60 ed i gradi di liberta' del sistema df=2,9 ma dobbiamo capire cosa stiamo facendo, il suo significato prima di andare a trovare questi valori in una delle cento tabelle di F disponibili sui libri.
| Sbg2 riflette la / misura la | Swg2 riflette la / misura la |
| variazione dovuta ai differenti shop + variazioni dovute al colore | variazione dovuta solo ai differenti shop |
| variazione dovute ai dadi + variazione dovute al giocatore | variazione dovute solo ai dadi |
| perdita di peso dovuta alle persone + perdita di peso dovuta all'esercizio | perdita di peso dovuta solo alla diversita' fra le persone |
| quanto lontano sono le medie di gruppo l'una dall'altra | quanto i punti variano rispetto alla loro media di gruppo |
L'idea di base e' che se c'e' piu' variazione fra i gruppi, between, che all'interno dei gruppi, within, allora possiamo dire che le medie sono differenti, i trattamenti producono differenze, i colori cambiano la vendita.
Prima definiamo un valore di confidenza per il nostro studio, di solito si usa il 95%, cioe' α=0.05. Con questo valore stiamo definendo una confidenza del 95% sulla veridicita' della nostra null hypothesis, accettando un errore del 5% che questa sia vera ma noi la definiamo falsa (errore di tipo 1).
Dato α ora bisogna andare ad individuare sulla curva della distribuzione F (tante curve per i vari gradi di liberta') il valore critico Fcr.
se F >= Fcr l'ipotesi H0 e' rigettata, i colori hanno influenza nelle vendite
Di tabelle ce ne sono tante, magari qualcuna pure sbagliata, vi consiglio questa by StatSoft da cui estraiamo: per α=0.05, per df=2,9 il valore Fcr=4.459
cioe' F=1.606 , Fcr=4.459 , l'ipotesi H0 e' accettata, i colori NON hanno influenza nelle vendite
Se questa slide non e' chiara magari quelle scritte da qualche altro ricercatore possono aiutare, sono migliaia, questo sono due che sembrano interessanti. Un esempio del Prof. Richard H. Hall at Missouri University, un esempio che ci servira', dal Prof. David Lantz at Colgate University (see also her courses).
| previous slide | next slide |