| Rome University, La Sapienza Chemistry Department Rome, Italy, Europe |
Dr. Giovanni Visco Cenni di statistica di base. Calcoli di regressioni e correlazioni. dicembre 2006 |
Corso di Laurea in Scienze Applicate ai Beni Culturali ed alla Diagnostica per la loro Conservazione |
| previous slide, 43 | next slide, 50 |
Chiudendo la correlazione fra variabili ricopiano in una slide riassuntiva tutti i descrittori di una correlazione. Anche se fino ad ora abbiamo usato praticamente solo OLS i seguenti mantengono il loro significato anche in ILS ed in OrLS pur con qualche modifica alle formule. Sperando che le formula ridisegnate qui siano le stesse di quelle viste nelle slide precedenti!
Le formule sono scritte pensando ad oggetti discreti, monete, vasi, etc., andrebbero completamente riscritte per variabili continue, magari con l'uso di integrali definiti (ma questo esula dall'Insegnamento, per ora). Inoltre stiamo lavorando, intrinsecamente, sul piano cartesiano ed usiamo la geometria euclidea (non siamo su un ovoide in coordinate polari).
Se volessimo davvero parlare della covarianza dovremmo prendere una sola popolazione, fare due campionamenti casuali con n estrazioni, confrontare le due serie di misure ottenute. Dovrebbero essere uguali provenendo dalla stessa popolazione e potremmo calcolare la sample covariance fra i due set con la formula. Ci aspetteremmo un forte correlazione.
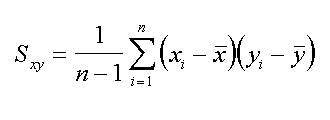 |
| sample covariance, true formula |
In cui: xˉ e' la media della prima serie di misure ed yˉ e' la media della seconda serie di misure. Sulla scrittura di n-1 ci sarebbe da discutere, esatta qui (e praticamente sempre usata da tutti) ma questionabile se si tratta di due variabili indipendenti, magari con covarianza prossima a 0, che di certo non corrispondono a quanto detto prima rispetto al metodo teorico di calcolo.
Riprendendo la definizione di covarianza vista qui sopra, cioe' partendo da una solo popolazione e facendo due campionamenti esaustivi si potrebbe confrontare con la formula qui sotto le due distribuzioni ottenute. Questa volta n e' la numerosita' della popolazione
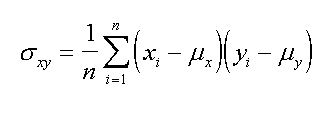 |
| population covariance, true formula |
Non e' che avete sbagliato lezione, non siamo a Filosofia della Scienza, non state leggendo Platone, Aristotele, Crisippo, Descartes, Bacon o Dupre ma qualche riflessione sulle formule che usiamo bisogna farla.
Dati gli assunti con cui abbiamo trovato questa formula il suo uso nella realta' sembra inutile. Eppure e' usata da molti per studiare una correlazione fra due variabili che hanno in comune solo "l'oggetto" sottoposto a misura. Pero', almeno, dovete avere a disposizione tutta L'Area Rilevata e misurare tutti gli oggetti. C'e' appena da ricordare che il valore numerico della covarianza dipenda dai valori delle due variabili.
Finalmente Karl Pearson, partendo dalle ricerche di Francis Galton, ha costruito un metodo per misurare la correlazione fra due variabili. Nessuna preventiva ipotesi e' necessaria, e' il testo stesso che ci dice se sono dipendenti od indipendenti.
 |
| true formula for Pearson-s product-moment sample correlation coefficient |
Veramente qualche presupposto c'e': le due distribuzioni non dovrebbero essere troppo lontane dalla gaussiana; la formula intrinsecamente suppone una regressione linare; la presenza di un outlier su una delle distribuzioni (e non sull'altra) falsa il test; un leverage point distorce completamente il risultato; il valore di rxy ha valori compresi fra -1 ed +1 ma i valori estremi sono "compressi" dai quadrati nella formula ed anche se non sembra 0.99 et 0.997 sono ben differenti. Ma tanto voi sapete che bisogna sempre graficare tutto!
La formula di calcolo e' facile. Qui di seguito a sinistra R2 ed a destra il Coefficient of Determination (qualche volta scritto com r2), ma e' il concetto che e' piu' complesso.
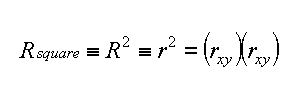 |
| coefficient of determination, square of Pearson's r |
A parte le tante rappresentazioni .... il Coefficient of Determination e' compreso fra 0 ed 1 e rappresenta la % di dati che e' descritta dalla correlazione (best fit), cioe r2=0.75 significa che il 75% della variazione della Y puo' essere spiegata con una relazione lineare fra Y ed X, il restante 25% rimane non spiegato.
Il coefficiente di determinazione e' utile perche' da' la proporzione della varianza di una variabile che e' prevedibile da l'altra variabile.
Ricrodando che R2 ha solo una valenza "analitica", "descrittiva", "comparativa", non ha un significato statistico come r. Percio' in ogni disciplina scientifica, in ogni modellazione, un coefficiente di determinazione pari a 0.83 puo' avere un significato oppure no. Ma per compararli?
Citando "... R2 alone cannot be used as a meaningful comparison of models with different numbers of independent variables. ...". Cioe' per comparare due R2 che contengono un numero diverso di osservazioni necessita un qualche aggiustamento statistico che tengo conto della numerosita' (anche se si trattano degli stessi oggetti del giorno prima meno uno che si e' perso). La formula di calcolo non semplificata e':
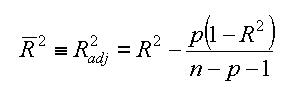 |
| adjusted R2 nelle sue varie notazioni |
Con le solite notazione per i simboli: n=numero di coppie di osservazioni, p=numero di variabili indipendenti (nel piano XY p=1), R2=coefficiente di determinazione. Sempre tenendo conto del suo significato, ora si possono compare due R2adj diversi con numerosita' diversa.
Calcolare l'errore associato ad r non e' facile. Nel lavoro e nalla formula di Pearson non c'e' traccia del calcolo dell'errore. Comunque eminenti statistici si sono cimentati in questo. E' qui il caso di ricordare che gli errori associati ad una misura sono spesso ottimi descrittori dei problemi nascosti in una misura (spesso piu' della misura stessa). Ecco due possibili formule.
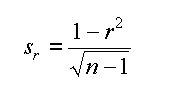 |
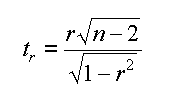 |
| assess of std.err. of Pearson's r | t values for r significance |
La formula a sinistra e' dovuta a Fisher (from ISBN 0-05-002170-2, 1925) e stima lo scarto quadratico medio in funzione della correlazione del campione non potendo usare la popolazione (vedere rslide10). Si noti il termine n-1 spiegato a lezione.
La formula a destra e' dovuta a Gosset e calcola il valore di t che con l'uso di qualche tabella ci da il valore di significativa' della correlazione. E qui si noti il termine n-2 anche questo spiegato a lezione.
Dato che trattasi di una correlazione lineare sara' stato calcolato il valore b^ di pendenza e a^ di intercetta da cui calcolare l'errore (sulla asse Y) di regressione per ogni punto. Dalla formula seguente,
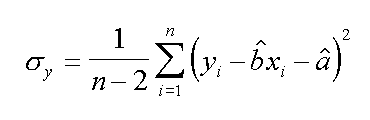 |
| variance of residuals (OLS regression) |
che calcola la varianza dei residui prodotti da una regressione OLS fra la variabile X e la variabileY.
Questo ed il successivo sono descrittori della qualita' di una regressione (e non solo) che si trovano spesso, mal presentati, nelle realzioni su correlazioni e regressioni.
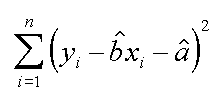 |
| RSS, residue sum of squares |
Un altro descrittore della qualita' di una correlazione, sempre partendo dai residui, che tiene anche conto del numero di campioni e' RMSD, calcolabile con la formula seguente. Ed anche qui ci sono questioni sulla divisione per n come riportato da tanti e tanti autori oppure per i gradi di liberta' della correlazione XY.
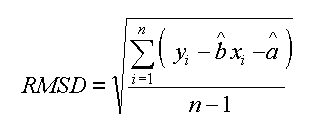 |
| RMSD, root mean square deviation (sample) |
E' l'errore sul valore di Y che viene stimato da una X misurata, mediante l'uso dei parametri b^ di pendenza e a^ di intercetta. La formula vale per OLS ed all'interno dello spread dei valori di X misurati.
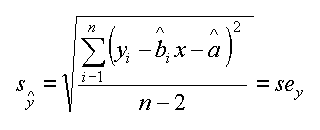 |
| standard error of the estimate Y |
Veramente il risultato sarebbe da associare solo alla Y^ in prossimita' del centroide della retta. Anche su n-1 oppure n-2 c'e' qualche differenza da un libro ad una altro, ma qui lavoriamo sempre con samples e non con population, ci sono due vincoli la pendenza della retta b^ ed il valore scelto di X.
E' l'errore sul valore di X che viene stimato da una Y misurata, mediante l'uso dei parametri b^ di pendenza e a^ di intercetta. La formula vale per OLS ed all'interno dello spread dei valori di X misurati (si non e' un errore di copia della riga sopra!).
| invece della formula questa volta un link ad un .pdf di Johannes Ranke |
| pag. 4, not so easy compute the standard error of the estimate X |
L'errore sul valore di X in predizione sarebbe quello che ci interessa di piu'! Ma abbiamo gia' visto con un esempio grafico che e' difficile da calcolare, ci servono almeno dei replicati (Y1, Y2, .. Yn per quella data X) e poi un po di statistica visto che partendo da OLS la X sarebbe nota senza errori!
L'uso di tutti questi descrittori contemporaneamente, unitamente con il grafico dei residui, permette di studiare "la qualita'" di una correlazione. Un grafico che raccolga questi valori a confronto permette di studiare un'ipotesi di linearizzazione.
| previous slide | next slide |