Correlazione non lineare e/o linearizzazione

  Appena qualche slide prima di questa abbiamo visto un esempio di covarianza e correlazione quasi nulla ma con dati che una volta presentati in un semplice grafico risultano ben "correlati" fra loro. Qualche volta una correlazione che non e' lineare puo' essere studiata (scoperta) dopo qualche trasformazione matematica.

  La linearizzazione e' possibile quando una funzione di correlazione e' lineare nei parametri anche essendo non lineare nelle variabili (y=a+bx+cx² oppure y= a+bLog(x)). Ma spesso il mondo reale presenta funzioni di difficile linearizzazione, come y=a*e^(-bx) del decadimento radioattivo ma anche alcune non linearizzabili, y=a*e^(-bx)+cx sempre un decadimento ma con nun fondo di un emettitore a lungo periodo.

  Galileo Galilei di certo non e' stato il primo a studiare la caduta di un grave ma pur facendo nascere con i suoi studi la Metodologia Sperimentale e la Riproducibilita' non aveva la nostra tecnologia. Ecco un link con un doppio significato: ottimo esempio di musealizzazione, descrizione di un opera.

  Veramente questo esempio non sarebbe corretto in quanto sappiamo gia' la relazione che lega le due variabili. L'esempio andrebbe bene per la sezione "regressione" ma tornate indietro nel tempo mentre ancora non era nota l'equazione del moto.

  Studiamo noi invece la caduta di un grave; prendiamo un sfera di un metallo molto denso, Osmio, installiamo su di un asse verticale una serie di fotocellule, una ogni 50mm, scegliamo un sistema di acquisizione dati con una risoluzione di 1 ms. Facciamo cadere il grave e leggiamo i tempi di attraversamento delle fotocellule (ma non eravamo tornati alla fine del 1500?). Non teniamo conto dell'aria, della latitudine e di tante altre cosette!

  In 0.45 secondi il grave ha gia' percorso 1 metro. Fermiamo qui l'analisi, avremmo bisogno di tante altre fotocellule e poi stiamo arrivando al limite della risoluzione.

distance (m) time (s) velocita' (m/s) time2 (s) 0.00 0.000 n.d. 0.000 0.05 0.101 0.50 0.010201 0.10 0.143 0.70 0.020449 0.15 0.175 0.86 0.030625 0.20 0.202 0.99 0.040804 0.25 0.226 1.11 0.051076 0.30 0.247 1.21 0.061009 0.35 0.267 1.31 0.071289 0.40 0.286 1.40 0.081796 0.45 0.303 1.49 0.091809 0.50 0.319 1.57 0.101761 0.55 0.335 1.64 0.112225 0.60 0.350 1.71 0.1225 0.65 0.364 1.79 0.132496 0.70 0.378 1.85 0.142884 0.75 0.391 1.92 0.152881 0.80 0.404 1.98 0.163216 0.85 0.416 2.04 0.173056 0.90 0.428 2.10 0.183184 0.95 0.440 2.16 0.1936 1.00 0.452 2.21 0.204304 1.05 ?? ?? ?? .... ?? ?? ?? 4.90 1.000 4.90 1 19.61 2.000 9.81 4

non lineare   Dato che la distanza fra le fotocellule e' fissa questo e' un tipico esempio di un sistema con un grado di liberta' in meno, mettiamo percio' la distanza sull'asse X ed il tempo misurato sull'asse Y. Mettiamo anche le barre di errore pari a due volte la risoluzione. caduta di un grave, secondi per percorrere un spazio noto si vede che c'e' una relazione ma non e' lineare allora linearizziamo   Cioe' andiamo a cercare se con qualche trasformazione matematica su una delle due variabili si ottiene una relazione lineare. Nel nostro caso proviamo con x2, cioe' con il quadrato del tempo impiegato dal grave. graficando non Y ma Y2 si ottiene una retta   Un grosso problema sono le barre di errore sull'asse Y. Si debbono ricavare i valori con la propagazione degli errori tenendo conto dell'equazione usata per linearizzare (anche per l'errore sull'asse X se e' linearizzato).

  Ora che abbiamo visto un esempio di linearizzazione forse e' bene ri-affermare che NON e' un bell'esempio, non trattasi di regressione per cui non sappiamo quale e' la funzione di trasformazione verso la linearita' (e non sappiamo nemmeno se esiste).

  Detto questo vediamo come potremmo procedere in un caso incognito di ipotetica correlazione fra due variabili:

• ottenere un gran numero di coppia di valori, non equispaziati ma scegliendo a caso per una delle variabili (la Y per esempio),
• se possibile analizzare i limiti di risposta (in sui si modifica l'andamento), per poterli escludere dal calcolo,
• graficare tutto, anche utilizzando le funzioni matematiche di trasformazione automatica degli assi che qualche software di statistica ha,
• ora e' il momento di ipotizzare quale funzione matematica potrebbe trasformare una variabile,
• data il gran numero di coppie di valori e le funzioni matematiche scelte si possono calcolare i parametri di correlazione fra una variabile non trasformata e l'altra,
• dai risultati si decide se una delle funzioni e' utile alla linearizzazione.

  Prendiamo l'esempio di prima e proviamo la linearizzazione confrontando Y , Log(Y) , Y² , e^Y.

  Iniziamo con la variabile Y non trasformata, cioe' il tempo misurato in ms. Di seguito i parametri della correlazione ed il grafico dei residui (con numeri/scala della Y mal scritta). Per il calcolo dei parametri possiamo usare lo spreadsheet CorrelationOLS.123 gia' visto qualche slides prima.

parameters (estimated with OLS method)	values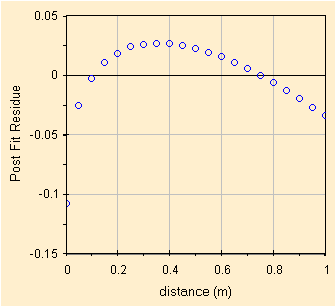
sample covariance	0.0363750
population covariance	0.0346429
Pearson sample correlation coefficient	0.9658713
square of the Pearson sample corr. coeff.	0.9329075
assess of Std Err of Pearson's r	0.0594238
variance of residuals	0.0010407
residual sum of squares (RSS), sample	0.0197729
root mean square deviation (RMSD), sample	0.0314427
degrees of freedom	19
standard error of the Y estimate	0.0322596

  Poi proviamo una linearizzazione trasformando la variabile Y in Log(Y). Chiaramente quando il grave e' fermo, cioe' distanza=0 non possiamo colcolare il Log cosi' abbiamo un punto in meno! Di seguito i parametri della correlazione ed il grafico dei residui.

parameters (estimated with OLS method)	values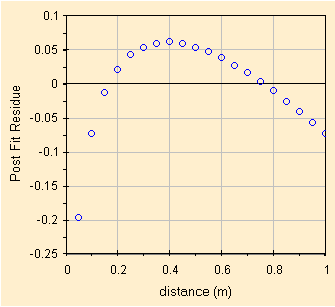
sample covariance	0.0485898
population covariance	0.0461603
Pearson sample correlation coefficient	0.9313267
square of the Pearson sample corr. coeff.	0.8673695
assess of Std Err of Pearson's r	0.0858392
variance of residuals	0.0043551
residual sum of squares (RSS), sample	0.0783925
root mean square deviation (RMSD), sample	0.0642333
degrees of freedom	18
standard error of the Y estimate	0.0659935

  Poi proviamo una linearizzazione trasformando la variabile Y in Y². Di seguito i parametri della correlazione ed il grafico dei residui.

parameters (estimated with OLS method)	values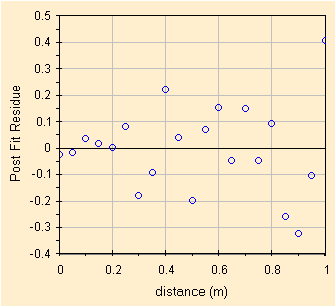
sample covariance	0.0196224
population covariance	0.0186880
Pearson sample correlation coefficient	0.9999965
square of the Pearson sample corr. coeff.	0.9999931
assess of Std Err of Pearson's r	0.0006036
variance of residuals	0.0000000
residual sum of squares (RSS), sample	0.0000006
root mean square deviation (RMSD), sample	0.0001664
degrees of freedom	19
standard error of the Y estimate	0.0001707

  Poi proviamo un'altra linearizzazione questa volta trasformando la variabile Y in e^Y. Di seguito i parametri della correlazione ed il grafico dei residui.

parameters (estimated with OLS method)	values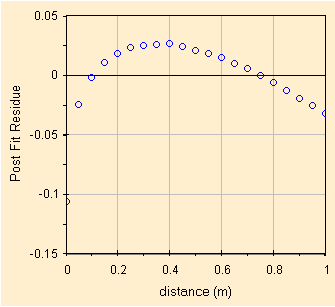
sample covariance	0.0478812
population covariance	0.0456012
Pearson sample correlation coefficient	0.9808538
square of the Pearson sample corr. coeff.	0.9620742
assess of Std Err of Pearson's r	0.0446777
variance of residuals	0.0009884
residual sum of squares (RSS), sample	0.0187796
root mean square deviation (RMSD), sample	0.0306427
degrees of freedom	19
standard error of the Y estimate	0.0314388

  Confrontando i risultati si nota che la trasformazione dell'asse Y in e^Y migliora un poco la correlazione ma la miglior linearizzazione si ottiene trasformando Y in Y² ottenendo un grafico dei residui da manuale (anzi che mostra come gia' ad 1 m si inizia a vedere l'aumento degli errori, forse da parte delle fotocellule).

  Per la linearizzazione si possono usare tante funzioni matematiche. In giro per internet c'e' una tabella con alcune funzioni matematiche, e' quella della Prof. Maria Teresa Garetto che nessuno cita mai per il suo Statistica Lezioni ed Esercizi. Leggete la tabella a pag. 55 e se volete il capitolo da pag. 49 a pag. 58. Purtroppo nel testo, interessante, NON ritroviamo nemmeno una volta la parola Validazione, e neanche Residui, ma nemmeno Predizione.

  Se avete solo poche coppie di dati e' probabile che riusciate con successo a linearizzarli con tante equazioni diverse. Per 4 punti puo' passare un cerchio, una parabola, un iperbole, una quadratica, etc., specie se i punti sono vicini e soggetti al rumore sperimentale. Per questo la linearizzazione necessita un Gran Numero di punti sperimentali per aver senso. Sapendole usare, le cosidette tecniche di Resampling potebbero aiutare se vi manca qualche punto.