| Rome University, La Sapienza Chemistry Department Rome, Italy, Europe |
Dr. Giovanni Visco Cenni di statistica di base. Calcoli di regressioni e correlazioni. dicembre 2006 |
Corso di Laurea in Scienze Applicate ai Beni Culturali ed alla Diagnostica per la loro Conservazione |
| previous slide, 41 | next slide, 43 |
Forse ne avremmo dovuto parlare molte slide fa', ma quando i punti sono cosi mal allineati che non siamo piu' capaci di trovare una retta che passa attraverso i nostri punti dobbiamo chiederci se davvero ci serve trovare una "retta".
RegressioneDefiniamo come regressione quel luogo di punti, una funzione Y = f(x), che descrive la variazione della variabile dipendente (Y) in funzione della variabile indipendente (X). Per la definizione stessa la funzione f(x) e' utilizzata in predizione per trovare quale valore di X produrrebbe un dato valore di Y misurato. Dopo tante misure in cui la variabile risposta (Ysperimentale) e' misurata a partire da una serie equispaziata di valori di X.
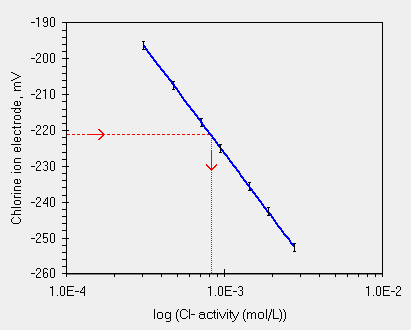
Uno dei tanti grafici gia' visti ci ri-presenta l'utilizzo della regressione.
 |
 |
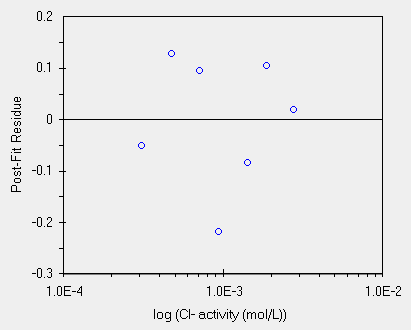
| avendo Y=221.3 la funzione Y=f(x) e' usata per predirre la x | ma quanto dista Ysperimentale da Ycalcolato? I residui |
Definiamo come correlazione una funzione Y=f(x) che descrive un relazione di mutua variazione fra due variabili misurate. Le variabili sono indipendenti (non legate cioe' da una legge gia' nota) e ad un tempo casuale sono misurate contemporaneamente. Come sapete tante piccole deroghe e tante variazioni sono possibili a questo assunto.
La correlazione e' statistica, cioe' usa metodi statistici di calcolo ed approssimazione per ottenere "la miglior curva" che correla i dati sperimentali ottenuti dalle due variabili fino ad un minuto prima ritenute "indipendenti".
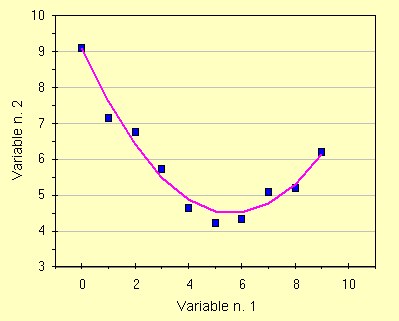 |
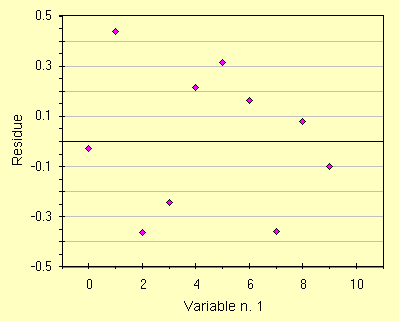 |
| con qualche formula della statistica otteniamo la curva viola | di cui stimiamo la qualita' con i soliti residui |
Anzi spesso non e' nemmeno dato il grafico ma solo un singolo valore numerico che si dice quanto sono correlati i dati sperimentali (ma rileggete due slide prima).
Definiamo come Interpolazione quell'insieme continuo di punti, collegati fra loro da una funzione matematica, che comprende/contiene al meglio i nostri punti sperimentali. Data la definizione il solito grafico aiuta a chiarire il concetto.
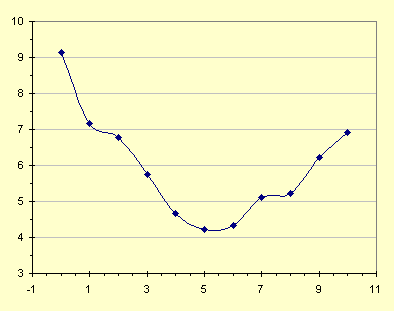 |
| interpolazione fra i punti con una polinomiale |
L'interpolazione e' matematica, cioe' matematicamente si puo' calcolare una funzione Y=f(x) che passi per TUTTI i punti, magari utilizzando polinomi di ordine superiore. Ma si capisce che questa non e' una correlazione e nemmeno una regressione.
| previous slide | next slide |