
| Rome University, La Sapienza Chemistry Department Rome, Italy, Europe |
Dr. Giovanni Visco Cenni di statistica di base. Calcoli di regressioni e correlazioni. dicembre 2006 |
Corso di Laurea in Scienze Applicate ai Beni Culturali ed alla Diagnostica per la loro Conservazione |
| previous slide, 40 | next slide, 42 |
Karl Pearson nel 1901 pubblico' un articolo su Philosophical Magazine n. 2 dal titolo On lines and planes of closest fit to systems of points in space che e' divenuto una pietra miliare della correlazione. Nell'articolo si fa riferimento al metodo per il calcolo del best fit mediante varie formule ed esempi di cui parleremo poi. Auguste Bravais aveva gia' evidenziato matematicamente la correlazione partendo da lavori precedenti di Francis Galton mediante il calcolo dei coefficienti relativi (see also Sir Francis Galton).
Qui abbiamo gia' studiato il coefficiente di correlazione. Purtroppo era stato utilizzato in modo improprio, ma sembra non ci siano altri stimatori semplici della bonta' di una regressione.
Qui invece e' il posto giusto per utilizzare il coefficiente, le due variabili sono indipendenti, la distribuzione di ogni variabile e' di tipo gaussiano, non siamo in presenza di una relazione nota ed attesa con variabile dipendente da una indipendente.
 |
| definizione del coefficiente di correlazione r |
Data l'indipendenza delle due variabili che vengono considerate nella correlazione, ed avendo gia' le definizioni di varianza e di covarianza possiamo ancora definire il coefficiente r
 |
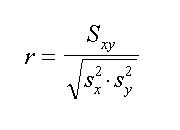 |
| altra definizione del r | data la covarianza e la varianza |
Da questa si puo' ricavare anche la definizione del coefficiente di determinazione r2 che potete trovare scritto anche come indice di determinazione:
r2 = misura la percentuale della variabilita' di Y spiegata dalla variabilita' di X
[The coefficient of determination represents the percent of the data that is the closest to the line of best fit. For example, if r=0.922, then r2=0.850, which means that 85% of the total variation in Y can be explained by the linear relationship between X and y (as described by the regression equation). The other 15% of the total variation in y remains unexplained.] from MathBits
| previous slide | next slide |