| Rome University, La Sapienza Chemistry Department Rome, Italy, Europe |
Dr. Giovanni Visco Cenni di statistica di base. Calcoli di regressioni e correlazioni. dicembre 2006 |
Corso di Laurea in Scienze Applicate ai Beni Culturali ed alla Diagnostica per la loro Conservazione |
| previous slide, 39 | next slide, 41 |
Come si vede anche dalla formula la covarianza misura una relazione lineare fra le due variabili, ma spesso esistono anche forti correlazioni seppur non lineari. Usiamo la covarianza per misurare la dipendenza di una variabile dall'altra.
Ne consegue che se due variabili sono indipendenti (oppure raccolgono valori casuali) la loro covarianza e' nulla. Bisogna fare attenzione a questa semplice affermazione perche' essa sottintende una relazione lineare (essa si basa sulla definizione di indipendenza stocastica espressa dall'equazione gia' vista). L'assenza di covarianza non implica che non ci sia un legame fra le due variabili.
Vediamo i dati ed il grafico di un primo caso, forse non molto clamoroso ma che ritroviamo spesso in chimica ed in biologia. Studiamo un'infezione batterica su di un'opera d'arte (libro, superficie pittorica, ecc.) contrastata dalla scarsita' di risorse, si ottiene una crescita quadratica, piu' lenta di quella esponenziale tipica. Prima scriviamo la tabella x-y
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| y | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
Ora disegnamo il diagramma di dispersione per queste due variabili. Ci attendiamo una perfetta correlazione avendo calcolato noi i valori di Y data la X.
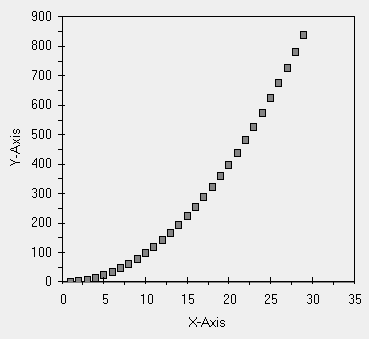 |
| La correlazione e' evidente |
Otteniamo i seguenti valori: r2=0.970 ed anche Sxy=2175. La covarianza e' molto elevata ma e' normale dati i valori elevati di Y, il coefficiente di correlazione "dovrebbe" essere 1. Pero' abbiamo gia' detto che queste formule sottintendono la linearita' e qui si vedono i primi errori.
Secondo caso, disegnamo un altro grafico questa volta davvero clamoroso. Prendiamo l'insieme dei punti del piano legati dalla relazione r2=x2+y2 nota ai piu'. Prima la tabella x-y.
| x | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 0 | +4.359 | +6 | +7.141 | +8 | +8.66 | +9.165 | +9.539 | +9.798 | +9.95 | +10 | +9.95 | +9.798 | +9.539 | +9.165 | +8.66 | +8 | +7.141 | +6 | +4.359 | 0 |
| y1 | 0 | -4.359 | -6 | -7.141 | -8 | -8.66 | -9.165 | -9.539 | -9.798 | -9.95 | -10 | -9.95 | -9.798 | -9.539 | -9.165 | -8.66 | -8 | -7.141 | -6 | -4.359 | 0 |
Nella tabella qui sopra, per problemi di spazio, le cifre significative sono sbagliate. Il disegno del diagramma di dispersione per queste due variabili e' facilmente riconoscibile. Ora ci attendiamo una perfetta correlazione, gia' ai matematici greci ed ancora prima in Mesopotamia era noto questo insieme di punti. Noi ci attendiamo una correlazione perfetta avendo calcolato i valori di Y data la X e seguendo l'equazione nota.
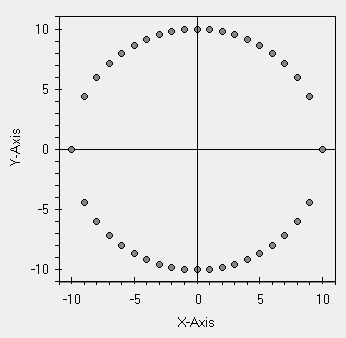 |
| E' stato inventato prima il cerchio o la ruota? |
Utilizzando il nostro amato foglio elettronico Lotus 123, utilizzando per i calcoli di y l'equazione esatta con 15 cifre decimali, applicando le formule gia' viste per la covarianza ed il coefficiente di correlazione, al limite degli errori di calcolo otteniamo i seguenti valori:r2=0.000 ed anche Sxy=0.000.
La covarianza e' nulla ed anche il coefficiente di correlazione e' nullo.
Ed ora cambiamo scenario, non avete un solo valore di covarianza ma una tabella con decine se non centinaia di valori che vi mostrano il "legame" fra le varie variabili misurate. Poniamoci nell'ottica di diffidare dai valori di correlazione piccolissimi o grandissimi e passiamo a studiare con un grafico questi casi prima di trarre conclusioni.
Tutto cio' fino a che non troveremo una formula per calcolare la covarianza non lineare.
| previous slide | next slide |