
| Rome University, La Sapienza Chemistry Department Rome, Italy, Europe |
Dr. Giovanni Visco Cenni di statistica di base. Calcoli di regressioni e correlazioni. dicembre 2006 |
Corso di Laurea in Scienze Applicate ai Beni Culturali ed alla Diagnostica per la loro Conservazione |
| previous slide, 38 | next slide, 40 |
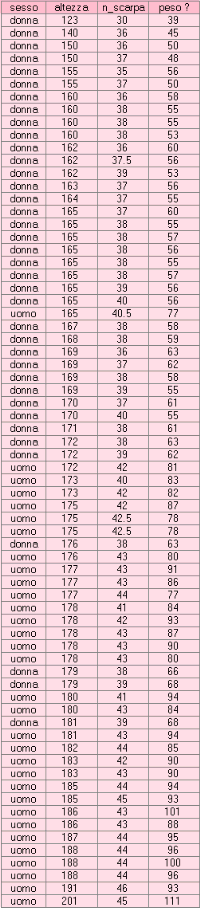
Ne abbiamo parlato nella prima slide sulla correlazione, del possibile legame fra altezza e numero delle scarpe. I miei studenti hanno provveduto a chiedere ad amici e parenti i dati necessari (speriamo) e su questi ci baseremo per i calcoli e le rappresentazioni. I 70 valori rilevati sono disponibili qui sulla destra.
Notiamo che abbiamo solo due variabili da rappresentare e percio' possiamo disegnare un diagramma di dispersione. Qualche autore chiama questo correlogramma, forse sbagliando, ma quello vero lo vedremo fra qualche slide. Quello qui sotto e' detto anche grafico X-Y.
Leggete per favore con attenzione questa definizione del Diagramma Di Dispersione the scatter charts is used to look for correlation between large sets of data. Use scatter charts only if your audience has the statistical knowledge to interpret them.. Oppure dovete essere voi a spiegarlo.

Come al solito le scale sono importanti. Ormai conoscete come si disegna un grafico X-Y, in questo caso abbiamo utilizzato tutta la lunghezza degli assi, le scale sono disegnate in modo da evidenziare bene i valori, i punti sono ben riconoscibili.
Il grafico X-Y [scatter charts, also called XY charts] evidenzia la relazione fra le due variabili. Esiste una correlazione positiva, un aumento della dimensione del piede (e cioe' del numero della scarpa da utilizzare) e' legato ad un aumento dell'altezza. Ora bisogna trovare qualche numero che evidenzi questa relazione e qualche altro mezzo che ci permetta di separare, se possibile, uomini e donne.
| general statistic values | X, meter | Y, feet n. |
| smallest value | 1.23 | 30.0 |
| arithmetic mean (average) | 1.713 | 40.3 |
| largest value | 2.01 | 46.5 |
| spread | 0.78 | 16.0 |
| sample, variance | 0.0129 | 9.7843 |
| sample, standard deviation | 0.1134 | 3.128 |
| sample, kurtosis | 2.3979 | -0.5682 |
| sample, skews | -0.695 | -0.2480 |
| most frequently occurring value | 1.65 | 38.0 |
| population, variance | 0.0127 | 9.697 |
| population, standard deviation | 0.1129 | 3.114 |
| population, kurtosis | 2.2390 | -0.5962 |
| population, skews | -0.6856 | -0.2447 |
| standard error of the sample mean | 0.0107 | 0.2956 |
| 95% magnitude of the confidence interval | 0.0209 | 0.5767 |
| difference% avg/mediane | -0.4065 | 0.1550 |
| harmonic mean | 1.7051 | 40.065 |
| geometric mean | 1.7092 | 40.19 |
| sample percentile, value at 5% | 1.55 | 36.0 |
| median value in list | 1.72 | 40.5 |
| sample percentile, value at 95% | 1.88 | 45.0 |
| interquartile difference (3^ - 1^) | 0.13 | 5.0 |
| counts measures (n. objects) | 112 | 112 |
| outliers, lower limit = avg - 3*std.dev | 1.373 | 30.9285 |
| trimmed mean, 99% | 1.7130 | 40.3125 |
| outliers, upper limit = avg + 3*std.dev | 2.0531 | 49.6964 |
| sample covariance | 0.295664 | |
| population covariance | 0.293025 | |
| Pearson's correlation coef. r | 0.8338326 | |
| Pearson coefficient of determination r2 | 0.695277 | |
| assess of Std Err of Pearson-s r | 0.052633 | |
| variance of post-fit residue | 3.008622 | |
| residue sum of squares (RSS), sample | 330.9484 | |
| root mean square deviation (RMSD), sample | 1.7267 | |
| degrees of freedom | 110 | |
| standard error of the Y estimate | 1.734538 | |
Anche esagerando un po con le cifre decimali, per prima cosa calcoliamo tutti i parametri statistici che conosciamo fino ad ora (vedi le oltre 100 slide precedenti) per ognuna delle due distribuzioni. Questo e' utile per far emergere qualche incongruenza che potrebbe falsare la correlazione. Poi calcoliamo quanto fino ad ora appreso sulla correlazione, la covarianza e' calcolata con la formula per un campione, gia' vista in precedenza e tanti altri parametri che vedremo poi. Partendo da questo data set, formato .123 et formato .XLS rilevato dagli studenti nel 2005.
The statistic parameters of a distribution and more and more paramenters of a correlation can be calculated by this spreadsheet. It is usefull to compute a table as above with parameters for distribution and correlation, this one CorrelationOLS.123 for Lotus and CorrelationOLS.xls for Excel. BE CAREFUL, the values are computed with internal functions of "your" spreadsheet, if there is an error in the algorithm you obtain BAD values.
| previous slide | next slide |