Misura della correlazione, covarianza [measure of correlation, covariance]

  Usiamo variabili a rapporti o variabili ad intervallo (parametriche). La prima misura della relazione fra due variabili (che definiamo come X ed Y) e' la covarianza [covariance]. Facendo riferimento alla lunga serie di slide sul campionamento ed anche alle lezioni possiamo affermare che se abbiamo misurato tutta la popolazione, per ambedue le variabili possiamo utilizzare la seguente formula per "calcolare" la covarianza.

  Diamo una bella definizione della covarianza: Covariance is the average of the products of deviations of corresponding values in lists.

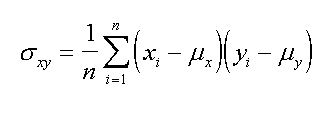misura della covarianza sulla popolazione

  Non misuriamo la popolazione ma solo una parte di essa, cioe' un campione. Con questo set di dati possiamo "stimare" la covarianza mediante la formula seguente.

  Se raffrontato al valore precedente si ottengono valori assoluti leggermente maggiori che come al solito differiscono meno se si ha un campione piu' esteso.

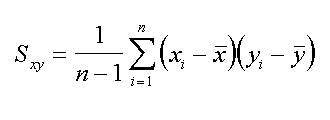misura della covarianza sul campione di X ed Y

  Un'altra misura della relazione fra due variabili e' la correlazione [correlation], il coefficiente e' gia' stato calcolato e la sua formula presentata nelle lezioni precedenti e lo riprenderemo in seguito. A queste possiamo aggiungere.

1. correlazione e covarianza misurano ambedue la relazione fra due set di dati
2. la correlazione e' indipendente dalle unita' di misura e mostra sempre valori compresi fra -1 (correlazione assoluta inversa) +1 (correlazione assoluta diretta) passando per lo 0 (correlazione nulla).
3. la covarianza dipende dalle unita' di misura e mostra con il suo valore anche la dimensionalita' delle variabili a cui si riferisce.