| Rome University, La Sapienza Chemistry Department Rome, Italy, Europe |
Dr. Giovanni Visco Cenni di statistica di base. Calcoli di regressioni e correlazioni. novembre 2005 |
Corso di Laurea in Scienze Applicate ai Beni Culturali ed alla Diagnostica per la loro Conservazione |
| previous slide, 20 | next slide, 22 |
Fino ad ora abbiamo studiato la risposta prodotta (la Y) da un sensore al variare di un parametro (la X). Pero' spesso la realta' e' molto diversa, una risposta (la Y) puo' dipendere dal valore di molte variabili (le X1, X2, X3, ecc.) anche correlate fra loro. Provate a disegnare i tre possibili grafici (X1-X2, X1-Y, X2-Y), sul piano cartesiano, e vedere cosa succede. Questi sono i dati.
| X1 | X2 | Y |
| 1.230 | 0.465 | 5.735 |
| 1.722 | 0.620 | 9.695 |
| 2.460 | 0.930 | 11.285 |
| 2.911 | 1.054 | 12.765 |
| 3.813 | 1.380 | 16.280 |
| 4.879 | 1.767 | 19.795 |
| 5.904 | 2.318 | 26.640 |
| 6.396 | 2.403 | 28.860 |
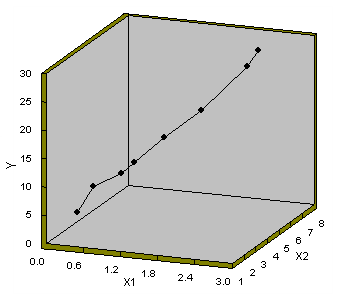
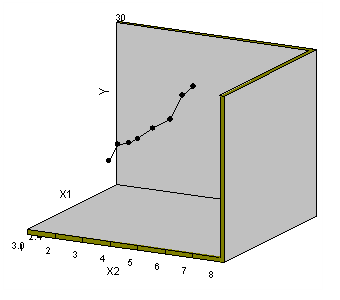
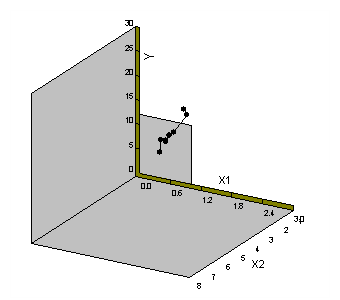
Ecco invece una rappresentazione X-Y-Z, notiamo che una variazione positiva della X1 produce un aumento della Y ma solo se nel frattempo si e' avuta anche una variazione positiva della X2.
 |
 |
| regressione bivariata Y=f(x1,x2) , vista prospettica | vista dal secondo asse delle X |
Le formula per calcolare la regressione sono simili a quelle gia' viste solo che in questo caso la y dipende da due variabili e non da una sola, come nell'equazione qui sotto.
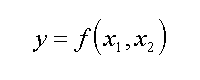
Nel caso particolare si otterrebbe una pendenza ed un termine noto per la X1 ed un altra pendenza ed intercetta per la X2. Nel nostro caso cioe' a1 et b1, ed insieme a2 et b2. Pero' non vi preoccupate i migliori programmi di statistica hanno tutte le routine per il calcolo della regressione multivariata ed anche il nostro amato Lotus 123 e' capace di far questo.
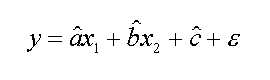
 |
 |
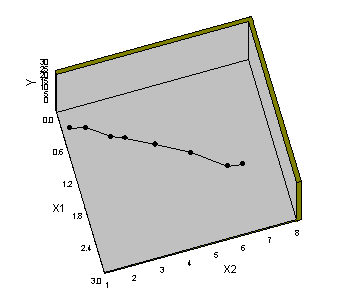
| vista dal piano X1 - X2 | vista dall'asse X1 |
Guardando il grafico di sinistra qui sopra si nota, in questo caso particolare, anche una forte correlazione (che cominciamo a studiare nella prossima slide) fra le due X. Ne riparleremo a lezione. Se vi interessano anche i valori numerici, questo e' il risultato:
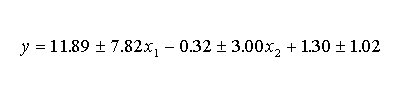
Come esercitazione potete ricavare gli altri 15 parametri di regressione partendo dai valori di X1, X2, Y mostrati nella tabella qui sopra.
| previous slide | next slide |