| Rome University, La Sapienza Chemistry Department Rome, Italy, Europe |
Dr. Giovanni Visco Cenni di statistica di base. Calcoli di regressioni e correlazioni. novembre 2005 |
Corso di Laurea in Scienze Applicate ai Beni Culturali ed alla Diagnostica per la loro Conservazione |
| previous slide, 15 | (large page > 200KB) next slide, 17 |
In alcune slide precedenti abbiamo presentato alcuni casi in cui l'errore e' presente anche sull'asse Y. Il caso dei valori della variabile indipendente, asse X, senza errore ci ha portato alla descrizione degli Ordinary Least Squares. Analizziamo anche altri due casi possibili utilizzando un nuovo set di dati, questo.
| Asse X | 2.193 | 1.743 | 1.244 | 0.899 | 0.544 | 0.344 | 0.185 | 0.097 | 0.039 | 0.020 | 0.010 |
| Asse Y | 2.001 | 1.703 | 1.098 | 0.901 | 0.507 | 0.301 | 0.203 | 0.085 | 0.042 | 0.017 | 0.010 |
Questo caso lo abbiamo gia' analizzato, purche' la variabile dipendente sia affetta da errori importanti e nel contempo la variabile indipendente sia invece misurata senza errore. Con i dati appena presentati si puo' disegnare il grafico qui sotto.
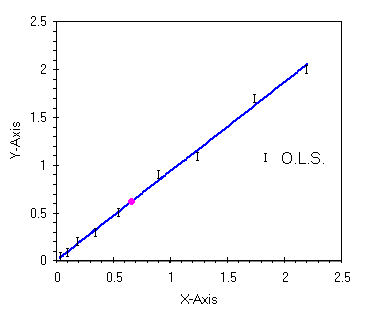 |
| il caso con gli errori sull'asse Y |
Per questo nuovo set di dati ecco nella tabella qui sotto i parametri di regressione calcolati con il foglio elettronico e con le formule gia' viste.
| Constant | 0.005 | Std Err of Constant | 0.018 | X Coefficient (slope) | 0.930 | Std Err of X Coef. | 0.018 |
| r coefficent | 0.997 | Assess of Std Err of r coef. | 0.019 | Std Err of Y Estimate (mediane) | 0.043 | Std Err of X Estimate (mediane) | 0.047 |
| Variance of residuals | 0.002 | Number of observations | 11 | Degrees of freedom | 9 | Barycenter, X value | 0.665 |
Specularmente al caso O.L.S. c'e' la possibilita' che la variabile indipendente sia affetta da errori importanti come grandezza e che la variabile dipendente sia invece misurata senza errore.
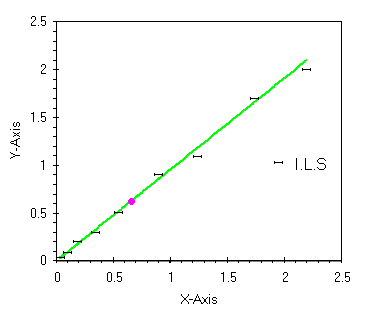 |
| il caso con gli errori sull'asse X |
Questa regressione in inglese e' detta Inverse Least Squares. Esistono formule matematiche per il calcolo di questa regressione. Non credo sia qui il caso di presentarle tutte anche perche' nel campo della chimica analitica (ma anche nelle misure chimico-fisiche) non e' molto utilizzata.
Il presupposto teorico e' che lo strumento di misura non e' affetto da errore e che invece la nostra conoscenza della variabile indipendente e' soggetta ad un errore non trascurabile.
Con il nuovo set di dati possiamo calcolare la regressione I.L.S. ed ottenere i parametri qui sotto mostrati, molto simili a quelli gia' visti ma con qualche differenza specie nei due termini dell'equazione.
| Constant | -0.004 | Std Err of Constant | 0.019 | X Coefficient (slope) | 1.071 | Std Err of X Coef. | 0.021 |
| r coefficent | 0.997 | Assess of Std Err of r coef. | 0.019 | Std Err of Y Estimate (mediane) | 0.047 | Std Err of X Estimate (mediane) | 0.044 |
| Variance of residuals | 0.002 | Number of observations | 11 | Degrees of freedom | 9 | Barycenter, X value | 0.665 |
Notiamo che r, con il numero di cifre da noi scelto, non cambia ed anche la varianza dei residui e' la stessa. Gli errori associati mostrano valori molto simili vista anche l'ottima correlazione. La pendenza e l'intercetta invece mostrano una piccola variazione che pero' ci darebbe un risultato ben diverso quando si dovesse calcolare una X in predizione partendo da un valore misurato di Y.
Vi sono vari termini per definire questa regressione, fra le tante citiamo, Orthogonal Least Squares, Total least squares, Orthogonal Regression, e Minimi Quadrati Totali. Qui si puo' generare qualche confusione, i vari testi di statistica qualche volta usano queste definizioni come sinonimi, altre volte ne evidenziano le differenze. Come primo approccio ci sembra il caso di individuare con questi nomi un diverso metodo di regressione senza fare troppe distinzioni.
Questo, finalmente e' un caso reale, molti sistemi di misura dovrebbero essere analizzati con questa regressione. I presupposti teorici, ampiamente condivisibili, sono i seguenti:
Facciamo un grafico con solo qualche punto del nuovo set di dati. Evidenziamo con la lente il valore X=1.244 , Y=1.098 e studiamolo con attenzione.
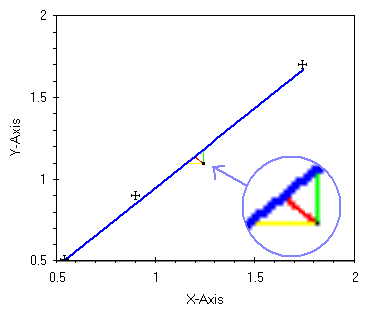 |
| un esempio di regressione ortogonale |
In nero vediamo il punto x,y. In blu una delle possibili rette di regressione. In verde ci e' gia' nota la distanza del punto dalla retta di regressione, minimizzando il quadrato di questa distanza, per tutti i punti, si ottiene la regressione O.L.S..
Il segmento in giallo e' la distanza del punto dalla retta di regressione con il metodo I.L.S.. Questa distanza, facile da calcolare, deve essere minimizzata per trovare la miglior retta di regressione con l'errore sull'asse X.
Se adesso guardiamo ai due segmenti, verde e giallo, come ai due cateti di un triangolo la cui ipotenusa e' il segmento blu possiamo disegnare il segmento rosso come bisettrice dell'ipotenusa (con un angolo di circa 45o al vertice fra il verde ed il giallo solo nel caso che i due errori siano di uguale valore).
Ora e' questo segmento rosso che dobbiamo minimizzare per calcolare Orthogonal Least Squares. Fra i tanti possiamo citare due casi, il primo in cui il segmento rosso e' sempre perpendicolare alla retta, blu, di regressione, l'altro in cui i due segmenti giallo e verde sono lunghi in proporzione all'errore associato alla X ed alla Y, rispettivamente cosi che il segmento rosso divida in due l'ipotenusa.
Purtroppo non esistono formule semplici per calcolare questa regressione. Si trovano varie soluzioni sui libri di statistica, tutte complesse. Con qualche conoscenza di geometria piana, con un poco di tecnica di programmazione, si potrebbe scrivere un programma che con la forza bruta trovi quali valori di a e b dell'equazione y=a+bx minimizzano il quadrato delle distanze misurate con la linea rossa (dopo aver deciso l'approssimazione richiesta).
| previous slide | (large page > 200KB) next slide |