| Rome University, La Sapienza Chemistry Department Rome, Italy, Europe |
Dr. Giovanni Visco Cenni di statistica di base. Calcoli di regressioni e correlazioni. novembre 2005 |
Corso di Laurea in Scienze Applicate ai Beni Culturali ed alla Diagnostica per la loro Conservazione |
| previous slide, 16 | next slide, 17b |
Uno dei problemi della regressione con i minimi quadrati (tutte e tre!) e' che un punto non allineato, detto in inglese Leverage Point, puo' modificare di molto i valori dei parametri di regressione. Abbiamo tutti il malvezzo di pensare ad una sola regressione sul piano euclideo, facile da graficare e con un Punto Anomalo ben visibile. Se invece abbiamo una matrice di correlazione oppure una regressione multipla non e' cosi' facile trovare un punto anomalo.
Vediamo tre possibili metodi per risolvere la regressione, metodo IUPAC della mediana, metodo Leave One Out, metodo Boostrap Analysis.
Leverage Points e Outliers sono diversiSi concettualmente sono diversi, ecco due possibili definizioni:
Prendiamo il set di dati usato in una slide precedente per la descrizione degli O.L.S. ed I.L.S.. Solo che chi ha trascritto i dati ha commesso un errore invertendo i valori 1.244 et 1.098. Un errore veniale che si potrebbe correggere riprendendo il quaderno di laboratorio e/o il piano di campionamento (avete tutto ben conservato, vero?). Solo che di questo errore bisogna prima accorgersene, come?
NON E' un buon set di dati, da un lato e' buono perche' il punto anomalo e' possibile, d'altro canto e' un cattivo set se confrontato con quello di tanti libri che presentano dati cosi' lontani dalla regressione che quasi tutti i metodi danno un buon risultato. In fondo alla pagina c'e' qualche grafico con questi esempi.
| Asse X | 2.193 | 1.743 | 1.098 | 0.899 | 0.544 | 0.344 | 0.185 | 0.097 | 0.039 | 0.020 | 0.010 |
| Asse Y | 2.001 | 1.703 | 1.244 | 0.901 | 0.507 | 0.301 | 0.203 | 0.085 | 0.042 | 0.017 | 0.010 |
| Point n. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Utilizzando tutti i punti, 11 compreso quello in azzurro, si ottiene una regressione i cui parametri si possono calcolare con il file di Lotus gia' presentato o con i tools di Excel. Questa regressione e' numericamente valida ma ERRATA giacche' di certo e' una stima molto approssimata.
| Constant | 0.015 | Std Err of Constant | 0.030 | X Coefficient (slope) | 0.954 | Std Err of X Coef. | 0.031 |
| r coefficent | 0.990 | Assess of Std Err of r coef. | 0.033 | Std Err of Y Estimate (mediane) | 0.074 | Std Err of X Estimate (mediane) | 0.077 |
| Variance of residuals | 0.005 | Number of observations | 11 | Degrees of freedom | 9 | Barycenter, X value | 0.652 |
Escludendo il punto in azzurro si ottiene una nuova regressione, con i dati mostrati qui sotto. Questa regressione seppur vera numericamente e' SOTTOSTIMATA in quanto e' calcolata con un punto in meno, il leverage point, sarebbe meglio calcolarla con un punto in previsione che sostituisca il dato anomalo. Pero' bisognerebbe aprire una discussione se e' piu' corretto rimuovere un dato o sostituirlo con la sua previsione (magari ne parleremo in un altro capitolo). E chi ci dice se l'errore e' sulla x o sulla y cosi' da poter calcolare il valore in previsione.
| Constant | 0.007 | Std Err of Constant | 0.016 | X Coefficient (slope) | 0.938 | Std Err of X Coef. | 0.017 |
| r coefficent | 0.997 | Assess of Std Err of r coef. | 0.018 | Std Err of Y Estimate (mediane) | 0.039 | Std Err of X Estimate (mediane) | 0.041 |
| Variance of residuals | 0.001 | Number of observations | 10 | Degrees of freedom | 8 | Barycenter, X value | 0.607 |
Leggendo la pagina 1009 del documento IUPAC citato piu' volte troviamo un metodo semplice ma discretamente efficace per stimare i veri parametri di regressione, proviamo a descriverlo in dettaglio.
Per due punti passa una retta (ma anche un cerchio, una ...). Il nostro set di dati, qui sopra, e' composto da 11 misure, il metodo qui presentato prevede il calcolo di tutte le regressioni fra due punti qualsiasi. Con 11 punti dobbiamo provare tutte le combinazioni senza ripetizione di 2 punti. Per esempio date quattro lettere a, b, c, d, scriviamo tutte e 6 le coppie di due lettere senza ripetizione, ab, ac, ad, bc, bd, cd, la formula e' la seguente, per n oggetti divisi in gruppi da r oggetti senza ripetizione:
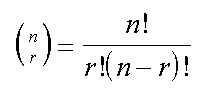
Nel nostro caso 11!=39916800 , 9!=362880 , da cui si ottengono 55 possibili combinazioni. Ora bisogna calcolare tutte e 55 le equazioni per le rette composte da due soli punti. La formula per l'equazione di una retta passante per due punti NON e' una regressione ma e' comunque molto semplice, vediamola:
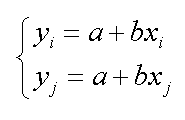
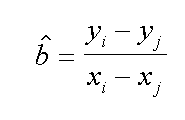
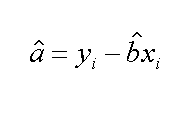
Sulla sinistra il sistema di due equazioni in due incognite, al centro una soluzione per trovare la pendenza della retta, sulla destra con una delle equazioni troviamo il termine noto. Con il foglio elettronico non e' difficile ma ci vuole un po' di tempo per impostare tutti i calcoli, ecco una tabella con i risultati. Se invece si dovessero calcolare i 496 valori dell'esempio dell'elettrodo al Cl-, con 32 punti x-y, sarebbe necessario un programma ad hoc.
| points | slope | intercept | points | slope | intercept | points | slope | intercept | points | slope | intercept | points | slope | intercept |
| 6-7 | 0.616 | 0.089 | 6-8 | 0.874 | 0.000 | 5-11 | 0.931 | 0.001 | 4-9 | 0.999 | 0.003 | 7-10 | 1.127 | -0.006 |
| 1-2 | 0.662 | 0.549 | 6-10 | 0.877 | -0.001 | 5-10 | 0.935 | -0.002 | 2-6 | 1.002 | -0.044 | 3-11 | 1.134 | -0.001 |
| 1-3 | 0.691 | 0.485 | 8-10 | 0.883 | -0.001 | 5-8 | 0.944 | -0.007 | 4-11 | 1.002 | -0.000 | 3-9 | 1.135 | -0.002 |
| 10-11 | 0.700 | 0.003 | 1-7 | 0.895 | 0.037 | 2-4 | 0.950 | 0.047 | 4-10 | 1.006 | -0.003 | 3-10 | 1.138 | -0.006 |
| 2-3 | 0.712 | 0.463 | 1-5 | 0.906 | 0.014 | 2-7 | 0.963 | 0.025 | 4-8 | 1.017 | -0.014 | 3-7 | 1.140 | -0.008 |
| 8-9 | 0.741 | 0.013 | 1-9 | 0.909 | 0.007 | 2-9 | 0.975 | 0.004 | 5-6 | 1.030 | -0.053 | 3-8 | 1.158 | -0.027 |
| 5-7 | 0.847 | 0.046 | 1-11 | 0.912 | 0.001 | 2-11 | 0.977 | 0.000 | 4-6 | 1.081 | -0.071 | 3-6 | 1.251 | -0.129 |
| 6-9 | 0.849 | 0.009 | 1-10 | 0.913 | -0.001 | 4-7 | 0.978 | 0.022 | 7-9 | 1.103 | -0.001 | 9-10 | 1.316 | -0.009 |
| 1-4 | 0.850 | 0.137 | 1-8 | 0.914 | -0.004 | 2-10 | 0.979 | -0.003 | 7-11 | 1.103 | -0.001 | 3-5 | 1.330 | -0.217 |
| 8-11 | 0.862 | 0.001 | 1-6 | 0.919 | -0.015 | 2-8 | 0.983 | -0.010 | 9-11 | 1.103 | -0.001 | 7-8 | 1.341 | -0.045 |
| 6-11 | 0.871 | 0.001 | 5-9 | 0.921 | 0.006 | 2-5 | 0.997 | -0.036 | 4-5 | 1.110 | -0.097 | 3-4 | 1.724 | -0.649 |
| slope (mediane value) | 0.975 | intercept (mediane value) | -0.001 | |||||||||||
Nella tabella qui sopra tutti i possibili risultati delle 55 combinazioni di slope ed intercetta.
La procedura per il calcolo della regressione robusta prevede ora il calcolo della mediana dei valori di b (lo slope) e la mediana del valori di a (l'intercetta). La retta di regressione e' come al solito y=a+bx. Per il calcolo degli errori su questa retta si rimanda alla bibliografia.
Il metodo funziona bene con leverage point davvero anomalo in quanto la mediana e' molto meno sensibile della media aritmetica nel considerare il valore centrale di una distribuzione in presenza di una forte coda.
Se c'e' un solo punto difettoso questa tecnica dovrebbe fornire buoni risultati. Si ripresenta sempre il problema di trovare uno stimatore della "bonta'" della regressione che ci permetta poi di decidere quale punto, escludendolo, migliora la regressione. Potete trovare questa statistica descritta, forse erroneamente, anche come JackKnife.
Ancora una volta con il foglio elettronico predisponiamo i calcoli per escludere uno alla volta i punti e ricalcolare tutti i parametri. Al termine riuniremo tutto in una tabella.
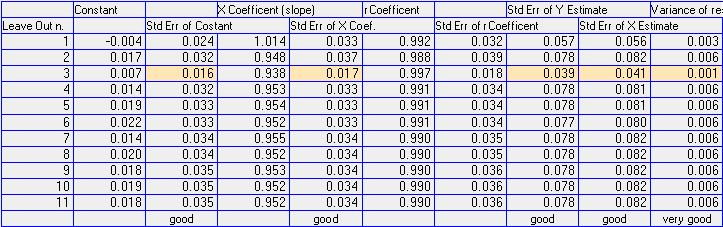 |
| i parametri di regressione calcolati con il metodo leave one out |
Analizziamo con attenzione la tabella. Levando il punto 3 tutti i parametri migliorano. Il miglioramento di alcuni, come il coefficiente di correlazione ed il suo errore, ci porterebbe in questo caso a risultati buoni ma sappiamo che e' meglio diffidare di questi come stimatore. Tutti gli altri errori sono invece utilizzabili.
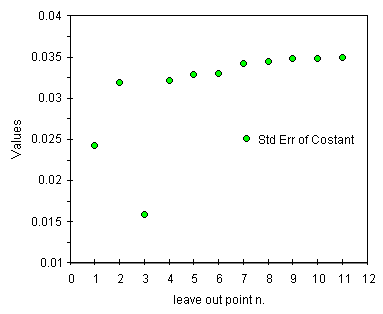
Osserviamo i valori degli errori descritti come good. Per il punto 3 tutti questi parametri mostrano un valore di circa la meta' del massimo, un buon risultato confermato anche dai grafici qui sotto. Per la varianza dei residui, descritta come very good, il valore senza il punto 3 e' invece molto piu' piccolo del massimo ponendo ancora piu' in evidenza questo punto e confermando gli altri.
 |
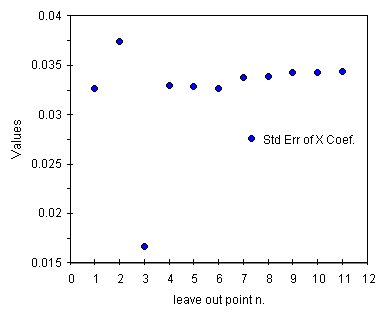 |
| andamento della deviazione standard della costante a | andamento della deviazione standard dello slope b |
 |
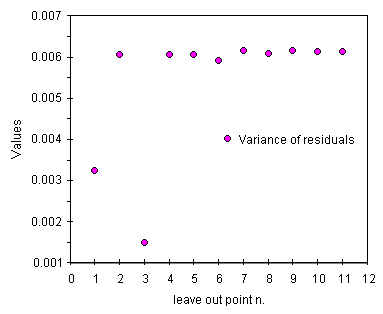 |
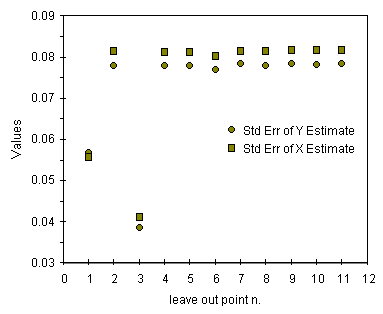
| andamento della deviazione standard delle stime su X et Y | andamento della varianza dei residui |
Il metodo funziona molto bene se si analizzano tutti i parametri. Possiamo vedere qualche problema su alcuni parametri per il punto 2 ma non su tutti. Anche il punto 1 e' da osservare ma continuiamo a tenerlo per estendere la risposta a basse concentrazioni.
Un metodo di indagine statistica piuttosto recente (se non sbaglio nata alla fine degli anni 70). In poche parole consiste nella definizione del nostro set di dati come "la popolazione" e nel campionamento Random Sampling With Replacement (gia' visto in molte slide precedenti) di questa popolazione.
Si sceglie percio' casualmente un piccolo numero di coppie di punti, la dimensione del campione e' anche essa casuale intorno ad un valore prefissato, la novita' e' nell'enorme numero di campionamenti, alcuni autori iniziano da 200 altri parlano di 100.000.
Nel caso in esame per 11 coppie di dati si potrebbe scegliere una dimensione del campione del 25%, cioe' 3 punti, selezionando percio' casualmente fra 2 e 4 coppie di dati. Pero' non si puo' certo parlare di regressione con due punti (e neanche con tre!), scegliamo almeno un numero fra 3 e 4. Ora un generatore di numeri casuali genera 5000 campionamenti (per esempio 4,2,9,11 e 7,4,1,7 e 6,3,10,2 e 6,7,9 e .....) si calcolano tutti i parametri e si producono le medie fra tutti i valori.
Esistono varie metodi di Bootstrap, non mi sembra qui il caso di analizzarli nel dettaglio, di certo ci ritorneremo. L'idea di base e' sfruttare intensamente il set di dati, sperando nell'emersione di una relazione nascosta e nella soppressione dei dati anomali da parte del rumore.
Un problema e' l'uso del foglio elettronico, senza programmazione delle macro o degli script non e' possibile far niente di tutto questo. Di certo, conoscendo a fondo gli algoritmi di calcolo, si puo' risolvere in Java o Phyton o meglio in Fortran o ancora nel magnifico APL.
Questo parte e' ancora da scrivere, ma per ora ecco un link con una descrizione semplice e comprensibile, in greco! (Prof. C.E. Efstathiou)
| previous slide | next slide |