blu, intercetta = -402.5, pendenza = -58.8, r = 0.998
| Rome University, La Sapienza Chemistry Department Rome, Italy, Europe |
Dr. Giovanni Visco Cenni di statistica di base. Calcoli di regressioni e correlazioni. novembre 2005 |
Corso di Laurea in Scienze Applicate ai Beni Culturali ed alla Diagnostica per la loro Conservazione |
| previous slide, 14 | next slide, 16 |
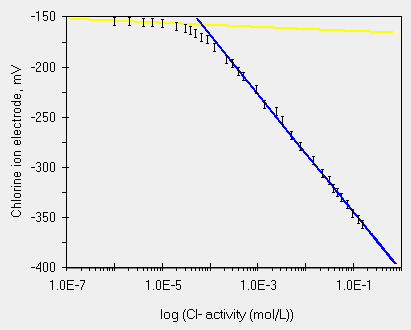
Se prendiamo la curva di risposta dell'elettrodo a Cl- dobbiamo trovare un sistema per escludere la zona di flesso (a basse concentrazioni) dalla zona di linearita'.
Analizziamo il problema, si possono individuare due rette nei punti ricavati sperimentalmente. Queste due rette le potete vedere nel grafico qui sotto. La retta gialla e' quasi parallela all'asse x, cioe' non c'e' risposta dell'elettrodo al variare della concentrazione. La retta blu e' quella gia' vista piu' volte, cioe' la risposta tipica dell'elettrodo al variare della concentrazione.
 |
| giallo, intercetta = -166.28, pendenza = 2.04, r = 0.968 blu, intercetta = -402.5, pendenza = -58.8, r = 0.998 |
A proposito, alcuni autori calcolerebbero il Limit Of Detection con il punto di intersezione fra la retta gialla e la blu. Il calcolo e' facile si tratta di trovare il punto di intersezione fra due rette, la coordinata Y non ci interessa, la coordinata X e' il valore del L.O.D. (per alcuni autori ed anche su alcuni documenti della IUPAC).
Fra la retta gialla e la retta blu c'e' una zona di flesso che e' tutta da studiare. Una tecnica usata in chemiometria per la validazione di un metodo e' il leave one out in cui uno alla volta vengono lasciati fuori dal calcolo i punti che hanno contribuito a sviluppare il modello stesso.
Per utilizzare la tecnica del leave one out ci serve uno stimatore che ci dica se il modello migliora o peggiora, cioe' ci dica se il modello senza questo punto sia migliore o peggiore. Vediamo per esempio la tabella qui sotto.
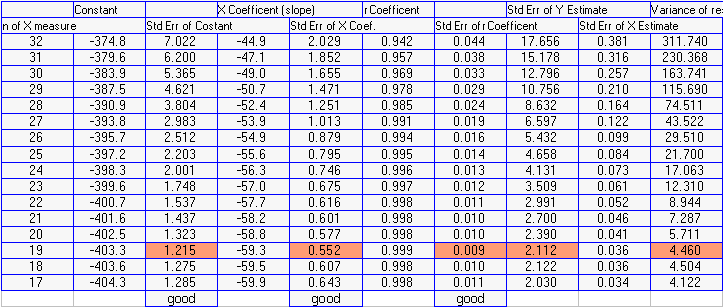 |
| una tabella con i parametri di regressione per l'elettrodo al Cl- |
Nella tabella sono riportati tutti i parametri che si possono calcolare per una retta di regressione (tutti no, solo i principali). Ora dobbiamo cercare un parametro che vari man mano che sottraiamo un punto. Sulla prima colonna a sinistra c'e' il numero di punti considerati. Stiamo via via lasciando fuori il punto a piu' bassa concentrazione. Le altre colonne mostrano i parametri di regressione.
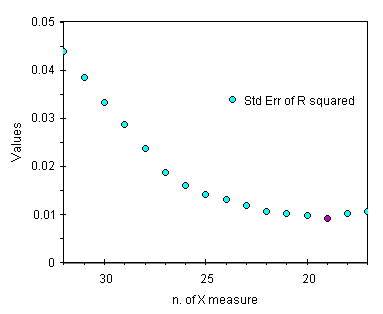
Cerchiamo una fra le colonne della tabella qui sopra che mostri un andamento non monotono. Nei grafici qui sotto ecco due esempi di parametri utili allo scopo.
 |
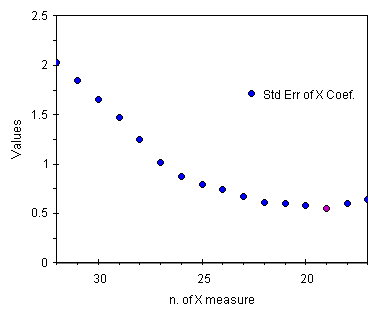 |
| andamento della deviazione standard di r | andamento della deviazione standard dello slope |
Scopriamo che al contrario dei parametri gli errori sono dei buoni stimatori della regressione. Nella tabella qui sopra sono stati evidenziati, in violetto, i punti di flesso. Con soli 19 punti si ottiene la migliore regressione. Diminuendo il numero di punti per sua stessa natura la regressione peggiora.
Pur se tutti i test individuano che con 19 punti si ha la migliore regressione un attento chimico analitico sceglierebbe di includere 20 punti. Includendo il punto dell'elettrodo da 2.24*10-4 moli/litro (invece di 3.02*10-4 moli/litro) si ottiene una miglior risposta alle basse concentrazioni senza perdere quasi nulla in termini di regressione, inoltre questo caso e' molto particolare dato il gran numero di valori di concentrazione utilizzati per studiare proprio la zona di flesso.
| previous slide | next slide |