Dicono che r non e' un buon stimatore! [someone affirms that r is not a good estimator!]

  Partiamo dalla definizione di r. Su tanti libri c'e' scritto correlation coefficient cioe' correlazione fra due set di misure, fra due variabili, fra due distribuzioni, pero' questa e' materia di alcune slide che seguiranno.

  Nel caso in questione si parla comunemente di variabile indipendente e dipendente con una forte relazione fra loro, non c'e' una distribuzione casuale dei valori della variabile indipendente (anzi scegliamo attentamente una sequenza di misure da eseguire).

  Abbiamo bisogno di un sistema per verificare se l'equazione che abbiamo calcolato descrive attentamente l'insieme dei punti. Tutta la struttura degli O.L.S. si basa sull'assioma che la X e' nota senza errore e che nella Y e' concentrato l'errore della misura. Possiamo sfruttare tutto cio'.

1. scegliamo con attenzione i valori di X;
2. misuriamo con cura i valori di Y;
3. applichiamo tutte le formule qui presentate per calcolare i parametri della regressione lineare;
4. riprendiamo i valori di X e calcoliamo i valori di Y come sarebbero se fossero davvero sulla retta;
5. ora facciamo la differenza fra questi valori di Y e quelli reali (i residui);
6. grafichiamo la X contro i residui.

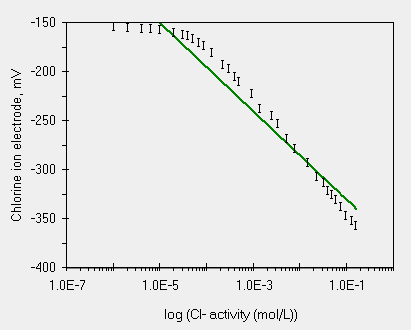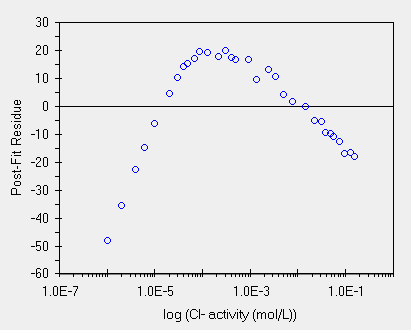una regressione scadente	ed ecco il grafico dei residui

  La regressione di sinistra e' davvero scadente, ed il grafico di destra lo mostra con facilita'. L'analisi dei residui evidenzia un forte andamento a campana con scostamento dal valore zero molto marcato fino al 8.6% (x = 235.5 , residue = 47.9). Non e' certo quello che ci si aspetta dai minimi-quadrati cioe' una distribuzione casuale dei residui.

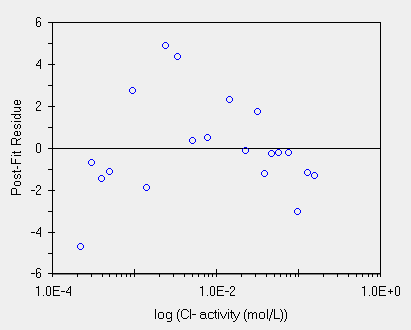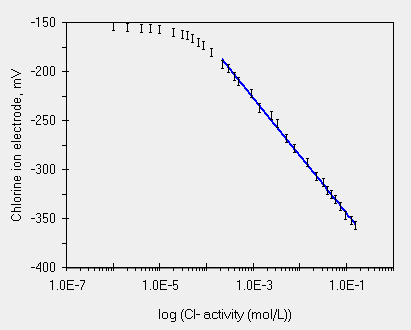
una buona regressione	ed il grafico dei residui, casuale

  Con un lavoro di eliminazione di punti si ottiene la regressione qui sopra a sinistra. E' davvero buona e l'elettrodo sembra seguire bene l'equazione di Nernst. Il grafico di destra mostra una distribuzione casuale dei residui, da mnuale. Anche il valore dello scostamento, 1.8% e' buono (x = 279.2 , residue = 4.9).

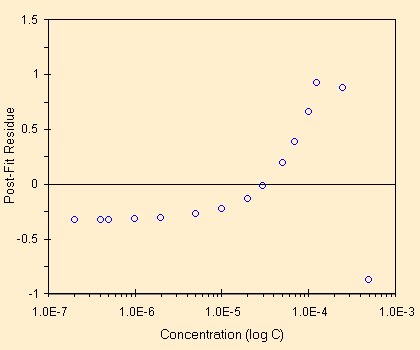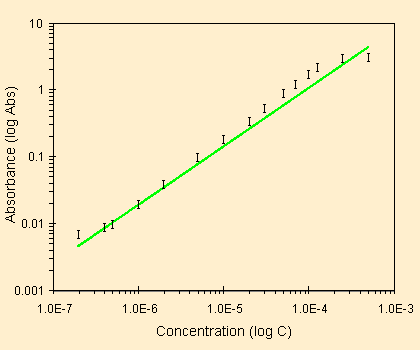
una regressione scadente	ed ecco il grafico dei residui

  Come abbiamo visto in alcune slide precedenti la regressione di sinistra e' sbagliata nelle concentrazioni piu' elevate ed invece non cosi errata come sembra in quelle piu' basse. Si tratta comunque di un andamento tipico, con il L.O.D. da un lato e la saturazione dall'altro. L'analisi dei residui evidenzia in modo inequivocabile questo andamento, non sembra proprio un andamento casuale, lo scostamento dal valore zero molto marcato fino al 29.2% (x = 3.190 , residue = 0.932). Il grafico dei residui non mostra come ci si aspetta dai minimi-quadrati una distribuzione casuale dei residui.

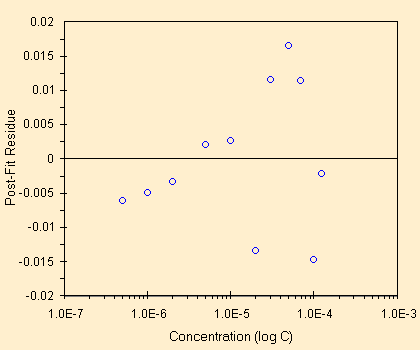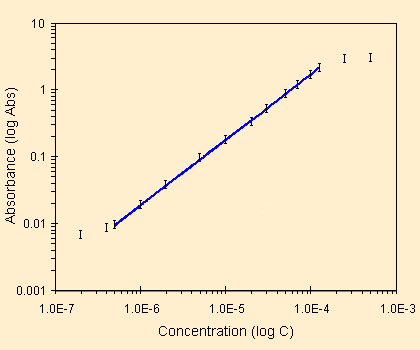
una buona regressione	ed il grafico dei residui, casuale

  Con un lavoro di eliminazione di punti si ottiene la regressione qui sopra a sinistra. E' davvero buona, lo spettrofotometro ben tarato, l'utilizzo del sistema di pesata diretta per le soluzioni sulla X, forniscono un valore di r di 0.999824037774026 (miracoloso se non fosse un cattivo stimatore!). Il tutto segue ottimamente la legge di Lambert-Beer.

  Il grafico di destra e' ancora una volta da manuale, si nota una distribuzione casuale, si nota il limite del L.O.D. con una mancata casualita' alle basse concentrazioni, un progressivo avvicinamento ai limiti dello strumento per le alte concentrazioni. Anche il valore dello scostamento, 0.77%, e' buono (x = 2.193 , residue = 0.017).

  Quello che ci manca e' un parametro che stimi la bonta' della regressione analizzando "visivamente" il grafico ed i valori dei residui e ci fornisca un numero da utilizzare. Molti statistici e chemiometri si sono cimentati in questa impresa ma per ora nessun "numero" e' diventato famoso come descrittore. Necessita sempre un'attenta analisi visiva sia alla forma sia ai valori sull'asse Y del grafico dei residui.

  Veramente uno ce ne sarebbe, PRESS (Predicted Residual Error Sum of Squares) ma in esso si parla di JackKnife e di altre cosette che vedremo poi.