Altri parametri per stimare la qualita' della regressione [estimation of regression's quality]

12. ellissoide di confidenza [confidence ellipse]: e' un altro valore statistico che misura la dispersione dei valori utilizzati per il calcolo della retta dalla retta stessa. Statisticamente si puo' poi ipotizzare che anche i dati reali rientrino in questa area con una probabilita' del xx%;
13. deviazione standard dell'intercetta [Standard Deviation of the Intercept]: e' un valore statistico che in funzione del numero di misure fornisce l'approssimazione dell'intercetta;
14. deviazione standard della pendenza [Standard Deviation of the Slope]: e' un valore statistico che in funzione del numero di misure fornisce la precisione della pendenza stimata;
15. deviazione standard dei residui [Residual Standard Deviation]: dopo aver calcolato la differenza fra valore misurato e valore teorico (ricavato dalla curva) per tutti i valori di y_i si calcola la deviazione standard di questa distribuzione;
16. deviazione standard del singolo valore di y in predizione [Estimated Standard Deviation of a Predicted Single Value y_r]: definiamo un qualsiasi valore di x e dalla retta di regressione estraiamo il possibile valore di y_r , cioe' in predizione. Quale sara' l'errore associato a questo valore;
17. deviazione standard del singolo valore di x in predizione [Estimated Standard Deviation of a Predicted Single Value x_r]: misuriamo un qualsiasi valore di y e dalla retta di regressione estraiamo il possibile valore di x_r , cioe' in predizione. Quale sara' l'errore associato a questo valore;
18. deviazione standard della media dei valori di x in predizione [Estimated Standard Deviation of a Predicted Mean Value x_r from n repetitions]: misuriamo piu' volte un valore di y, dalla retta di regressione estraiamo i possibili valori di x_r , cioe' piu' predizioni. Quale sara' l'errore associato al valore medio di x_r.

  Passiamo ad analizzare uno ad uno questi parametri. Il numero 13 ed il numero 14 sono gia' stati visti nella slide precedente. Misurano lo scarto quadratico medio dei valori a e b dell'equazione y=a+bx+e.

  Anche il numero 15 e' utile per stimare se la regressione e' valida oppure no e sara' descritto in seguito.

  Un commento a parte meritano i punti 16 et 17. Una volta trovati i due termini dell'equazione della retta possiamo sia calcolare il valore della variabile dipendente dato un valore noto della variabile indipendente sia misurare un Y ed ottenere il possibile valore di X che produrrebbe questo numero.

  Tutti i parametri gia' visti come il numero 5, il 6 et 9, il 7 et 10, lo 8, il 15, il 16 e necessariamente il 17, devono essere sempre riportati quando si descrive una regressione, molti fogli elettronici hanno upgrade oppure ad-on che li calcolano oppure usate queste formule.

  Prendiamo il grafico qui sotto, mostra proprio questo aspetto (forse non molto usato in "analitica") in cui per un valore noto di x si ipotizzano tutta una serie di valori di y poiche' i due termini dell'equazione della retta portano associato un errore, seppur piccolo nel nostro caso, sono stati evidenziati due possibili valori di y_r prodotti da due fra le tante possibili rette di regressione.

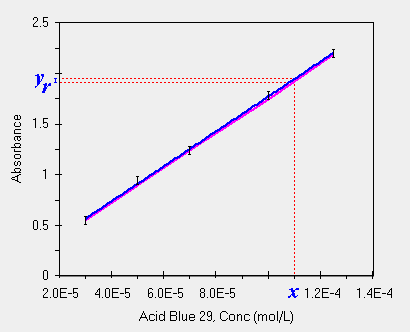trovare il valore di Yr partendo dalla X

  La formula si puo' trovare in vari testi di statistica e/o sulle raccomandazioni citate in bibliografia, la piu' semplice e' la seguente:

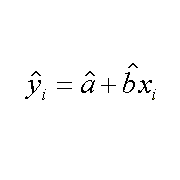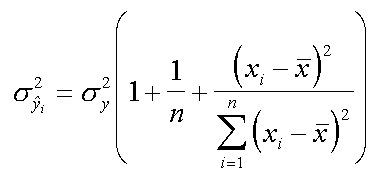calcolare il valore di y	e la varianza associata alla y calcolata

  Notiamo che la varianza e' funzione di x_i cioe' da quanto il valore di x e' lontano dal centro del suo range. Detto ancora meglio con pochi punti, molto distanti fra loro si ottiene poi una stima scadente di y, stima che comunque peggiora sempre man mano che ci si allontana dal centro della retta (il baricentro).

  Alcuni programmi di fitting presentano come dato il valore dello scarto quadratico medio calcolato sul valore mediano di x, (cioe' quello piu' vicino alla media artimetica di x). Meglio che niente ma comunque un valore ottimistico.

  L'ellissoide di confidenza rappresenta graficamente proprio questo aumento dell'errore allontanandosi dal baricentro. Vedi questo grafico ricavato da un famoso testo di statistica.

  Ben diverso e' il grafico qui presentato. Possiamo affermare che tutto il tempo fino a qui utilizzato per calcolare la retta di regressione (nel nostro caso con O.L.S.) sia stato speso proprio per risolvere questo caso.

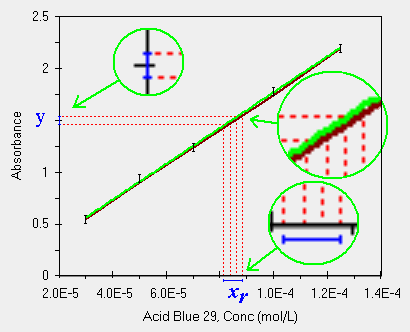trovare il valore della Conc dato il segnale

  Iniziamo dal valore di y misurato con l'errore associato uguale a quello utilizzato nella regressione, caso omoscedastico, notiamo la lente in alto a sinistra che ci indica un valore di assorbanza pari ad 1.5. Le due linee rosse ci mostrano questo valore di y riportato sulle possibili rette di regressione (due sole mostrate fra le tante) tenendo conto dell'errore associato ai parametri a e b. Nella lente in mezzo a destra.

  Finalmente tutti questi punti di intersezione fra i valori di y e le possibili rette vengono riportati sull'asse x ottenendo un valore di x_r di poco superiore a 8.0 x 10^-5 e di poco inferiore a 9.0 x 10^-5. Questo e' quello di cui avevamo bisogno, registrare un valore di y ed ottenere dalla retta il valore della concentrazione, su x.

  Anche questa formula si puo' trovare in vari testi di statistica e/o sulle raccomandazioni citate in bibliografia, la piu' semplice e' la seguente:

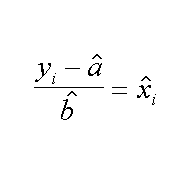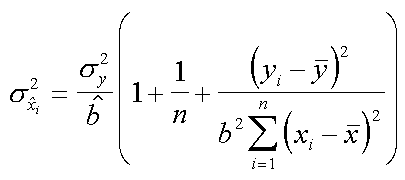calcolare la x attesa	e la varianza associata alla x calcolata

  Ancora una volta notiamo che il valore dell'errore e' associato ad un dato valore di y_i, cioe' varia al variare della distanza fra y_i e la media della variabile dipendente. Punti al limite della curva avranno errore maggiore. Una eventuale estrapolazione non farebbe che peggiorare l'errore.

  Alcuni programmi di fitting presentano anche per questo valore lo scarto quadratico medio calcolato sul valore mediano di x, (cioe' quello piu' vicino alla media aritmetica di x). Meglio che niente ma comunque un valore ottimistico.

  Ricordiamo che dopo tanta fatica e' questo quello che volevamo ottenere:

1. costruiamo tanti valori di x_i, concentrazioni;
2. misuriamo la risposta del metodo-strumento-sensore, ottenendo y_i;
3. matematicamente confermiamo una retta di regressione nota (Nernst, Lambert-Beer, ecc), trovando i parametri;
4. misuriamo una concentrazione incognita che ci fornisce una y;
5. dall'equazione della retta, finalmente, otteniamo il valore di x e l'errore associato.

  Per ottenere tutti questi parametri potete utilizzare il file regressionOLS.123 che prevede sia una pagina per la regressione lineare sia una pagina per la regressione log( x ). Sono previste 23 coppie di valori ma potete aggiungere o sottrarre righe (in mezzo, per favore) fino a raggiungere il numero richiesto.

  Per Excel ci stiamo lavorando (versione preliminare regressionOLS.xls), nel frattempo potete usare un Add-Ins che e' disponibile per tutte le versioni da 97 in poi. Se lo avete installato troverete in Tools ---> Data Analysis ---> Regression tutto quello che serve, purtroppo con poche spiegazioni sui risultati che si ottengono. Se cercate su Internet potreste trovate pero' qualche professore che nelle sue lezioni vi descrive i risultati presentati.