I parametri di regressione [regression's parameters]

  Prima di presentare le formule relative al calcolo della regressione e di analizzare i limiti e le potenzialita' della regressione sul piano euclideo e' meglio dare alcune definizioni.

  Quando si scrive un risultato di una regressione sarebbe meglio calcolare sempre anche i valori per tutti questi parametri (ed anche quelli fra due slide!):

1. numero delle osservazioni [number of observations]: cioe' il numero di punti misurati su ognuno degli assi, nel nostro caso il numero di concentrazioni sotto indagine. Di solito un numero dispari di valori, equispaziati (il classico 1-2-5-10-20....), alcuni autori parlano di almeno 7 valori, altri di almeno 13-15 che pero' NON sono sufficienti per stimare tutto l'intervallo di misura;
2. gradi di liberta' [degrees of freedom]: il numero delle osservazioni meno il numero di variabili indipendenti (meno il numero di ripetizioni);
3. variabile indipendente [independent variable]: la quantita' il cui valore puo' essere scelto arbitrariamente dall'operatore. Il valore va posto sull'asse X;
4. variabile dipendente [dependent variable]: la quantita' misurata e graficata in funzione della variabile indipendente. L'operatore non ha controllo su questa variabile ma puo' solo registrare i suoi valori. E' anche detto valore osservato e va posto sull'asse Y;
5. equazione di regressione [regression equation]: e' l'equazione che linearmente descrive la retta di regressione. La forma estesa e' y=a+bx+e;
6. intercetta [constant or intercept]: e' il parametro a nell'equazione precedente. E' anche detto termine noto. In chimica e' il valore della variabile dipendente misurato in assenza di analita (dovrebbe !);
7. pendenza [X coefficient or slope]: e' il parametro b nell'equazione precedente. E' funzione della sensibilita' del metodo di misura;
8. coefficiente di correlazione r [ r, or correlation coefficient]: e' un termine che statisticamente misura l'associazione fra le due variabili. E' spesso mal utilizzato in quanto e' solo un dato statistico che non descrive il vero andamento della curva;
9. errore sull'intercetta [standard error of constant (intercept)]: come al solito ad ogni valore deve essere associato un errore (qui lo scarto quadratico medio). Questo e' l'errore, in previsione, con cui calcoliamo l'intercetta;
10. errore sulla pendenza [standard error of X coefficient (slope)]: anche qui bisogna calcolare l'errore associato alla pendenza, nella stessa forma vista qui sopra;
11. errore sul coefficiente di correlazione [standard error of correlation coefficient]: quasi mai usato, pero' utile, calcola (approssimando secondo vari autori) l'errore associato al coefficiente di correlazione, nella stessa forma vista per gli altri due parametri.

  Esistono tanti parametri per stimare la qualita' della regressione (ellissoide di confidenza, errore standard sui valori di X regrediti, residui stimati, ecc.) ma ne parleremo fra 3 o 4 slide !

  Queste sono le formule che dovrebbero essere usate da tutti i programmi per il calcolo dei valori di intercetta e pendenza nel caso di regressione O.L.S.

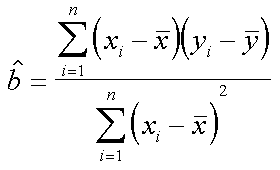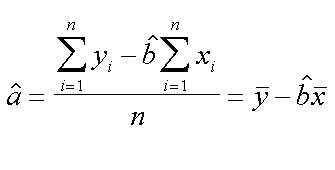prima il calcolo della pendenza	poi con una delle formule, l'intercetta

  Possiamo adesso calcolare la relazione fra due variabili casuali. Necessita la citazione della pagina 73* "the correlation coefficient ..... has no meaning in calibration under the condition mentioned above because the values x are not random quanties ....".

formula statistica per il calcolo del coefficiente di correlazione

  In presenza di dati replicati (cioe' ripetendo la misura sulla medesima concentrazione, usando la ripetibilita' a breve dello strumento) si possono inserire tutti nella regressione e forse avvicinarsi un poco alle raccomandazioni IUPAC.

   Lo studio dei dati replicati e' invece fondamentale per la chemiometria della regressione, una giusta applicazione di questi ci fornisce altri valori sui gradi di liberta', sull'accuratezza con cui abbiamo calcolato i parametri, sul funzionamento dello strumento, sulla qualita' dei dati anche sull'asse X, ecc.. Se ne parlera' in una slide finale.

  Finalmente abbiamo ottenuto una equazione della retta di regressione nella sua forma estesa. In essa vediamo a sinistra il valore che si avrebbe per una qualsiasi Xi (senza errore!), a destra vediamo quale e' invece il valore di Yi vero. Con il metodo O.L.S. abbiamo proprio minimizzato il valore di Ɛ_i.

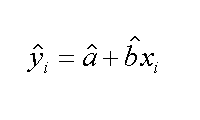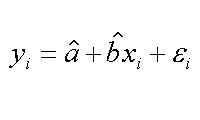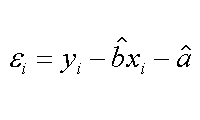il valore teorico di Yi, dalla retta	il valore reale di Yi, con l'errore	il valore dell'errore, da studiare

  L'analisi di questi valori di Ɛ_i ci permettera' di trovare molti altri parametri per studiare la bonta' della regressione e gli errori associati ai parametri fino a qui presentati.

  Ed ora le formule per calcolare l'errore sull'intercetta e l'errore sulla pendenza. Ricordiamo che trattasi di errori in previsione. Un altro aspetto che permette di trovare una soluzione univoca deriva dalla definizione stessa di O.L.S. cioe' che delle coordinate (x_i,y_i) la x e' nota senza errore.

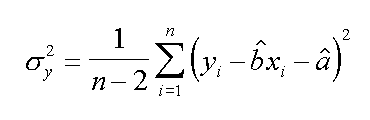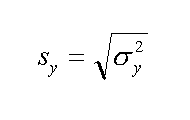la varianza dei residui	lo sc. quad. med. dei residui

  Nella formula per il calcolo della varianza dei residui usiamo n-2 in quanto sono noti sia a che b. Come al solito la radice della varianza e' lo scarto quadratico medio (std. dev.).

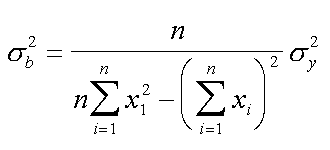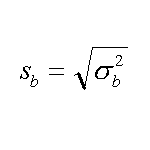la varianza dello slope	sc. quad. med. dello slope

  Finalmente la formula qui sopra per il calcolo dell'errore (sc. quad. med.) da associare al coefficiente della X, che nel nostro caso e' detto slope, la b.

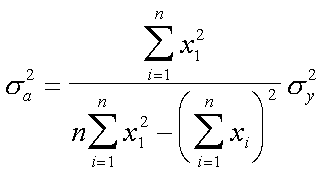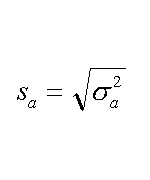la varianza dell'intercetta	sc. quad. med. su intercetta

  Nella formula qui sopra, il calcolo dell'errore (sc. quad. med.) da associare al termine noto dell'equazione y = a + b x , cioe' ad a.

  Qui le cose si complicano (se ce ne fosse bisogno), gia' il coefficiente di correlazione non e' un buon stimatore per la regressione, poi per calcolare la sua varianza i valori dovrebbero seguire una distribuzione normale e essere casualmente distribuiti, ma questo porta quasi per definizione ad un r=0, caso che non ci interessa.

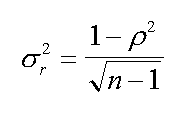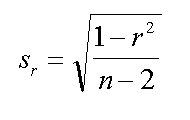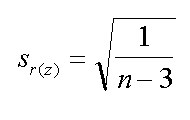la varianza teorica di r	stima dello sc.quad.med. di r	stima di Fisher dello s.q.m. di r

  Tanti statistici fra cui Fisher, Gosset, Mudappur, Jeyaratnam, si sono cimentati nel trovare un intervallo di fiducia intorno al valore di r.

  La formula di sinistra e' quella teorica della varianza di r, valido per r prossimo allo 0. Di questa formula non e' noto il valore di rho, il coefficiente di correlazione della popolazione.

  La formula di centro approssima il valore dello scarto quadratico medio di r per piccolo numero di campioni e per valori di r molto elevati. Usa la statistica di Gosset (cioe' puo' essere usata dove e' valida una distribuzione di Student).

  La formula di destra sarebbe utilizzabile per r prossimi ad 1 (come nelle rette di calibrazione in chimica e fisica), mi sembra dovuta a Fisher, prevede molte considerazioni sulla regressione che non e' qui il caso di trattare.

  NESSUNA di queste fornisce un calcolo rigoroso, non si trova nei principali software di regressione, ma di solito la formula al centro fornisce almeno un valore di stima.

  E' appena il caso di ricordare che molte di queste formule sono gia' comprese nei principali fogli elettronici (Lotus 123, Open Office, ecc) e che se ne mancasse una si puo' facilmente risalire al valore con tutte le altre funzioni del foglio, somma di quadrati, ecc.. Ne riparleremo in una prossima slide.

  Tanti, pieni di formule, alcune davvero importanti, alcune ben scritte, altre incomprensibili. Nelle prossime slide qualche riferimento a libri e pagine web. Come sempre per primo il riferimento alla IUPAC. Leggete in ogni caso l'elenco completo alla fine di queste slide.

1. *K. Danzer, L. A. Currie, Guidelines for Calibration in Analytical Chemistry Part 1: Fundamentals and Single Component Calibration (IUPAC Recommendation 1998), Pure and Applied Chemistry, 70(4) pp 993-1014, 1998, (1.06 MBytes).
2. K. Danzer, M. Otto, L. A. Currie, Guidelines for Calibration in Analytical Chemistry. Part 2: Multicomponent Calibration, Pure Appl. Chem. 76(6), 1215-1225, 2004, (250 KBytes)
3. IUPAC, Orange Book, Chapter 2, Section 4, Quantities Related to the Use of Linear Calibration Functions, 1999, la copia sul nostro sito, .PDF file (28917 Bytes).
4. Lezioni del Prof. R. Casa, Universita' della Tuscia, la lezione n. 5 pag 22. Potete comunque leggere anche le altre lezioni di Metodologia Sperimentale.
5. Belle pagine del Dr. Tom Kirkman (from College of Saint Benedict, Saint John's University) Least Sqares, oppure la pagina di Statistic to use con anche vari on-line calculator (citiamo anche Tools for Science, incompleto).