Definizione di regressione

  La definizione di regressione e' molto piu' ampia di quella che diamo qui. Una definzione estesa potrebbe essere "trovare una curva Y=f(X_i,j) che meglio descriva un insieme di punti (X_i,j), nel piano o nello spazio, e che possa essere ustata per ricavare uno qualsiasi X, compressa nell'intervallo studiato, a partire da una Y nota".

  In tutte le prossime slide parleremo di Classical Least Squares (CLS) e non di tanti altri metodi qualche volta necessari ma piu' complessi come Multiple Linear Regression (MLR), Pricipal Component Analysis Regression (PCR), Partial Least Square Regression (PLS), Locally Weighted Regression (LWR), Robust Regression Analysis (RRA), Projection to Latent Structures (PLS2), Orthogonal Projections to Latent Structures (OPLS).

  Alcune di queste le tratteremo in altri capitoli. Forse e' il caso di ricordare che non bisogna confondere queste regressioni con quelle usate per lo Smoothing, magari usano gli stessi algoritmi ma lo scopo e' ben diverso!

  Una dei possibili metodi per trovare un'equazione che descriva la relazione fra X ed Y e' la O.L.S. anche detta Ordinary Least Squares oppure in italiano Metodo dei Minimi Quadrati.

  Prima di procedere ancora una volta bisogna parlare degli errori associati alle misure, possono essere di due tipi:

1. omoscedastici [homoscedastic]: gli errori hanno una distribuzione di tipo gaussiano e il loro valore e' costante per tutti i valori sia per la variabile dipendente che per la variabile indipendente;
2. eteroscedastici [heteroscedastic]: gli errori hanno una distribuzione di tipo gaussiano ma il loro valore varia al variare dei valori di Y.

  Sono proprio gli errori, cioe' la non perfetta conoscenza del valore delle coordinate dei punti Xi-Yi che ci permettono di disegnare una retta che si avvicini ai punti tenendo conto della loro possibile, reale, posizione sul piano.

  Forse puo' sembrare una considerazione di filosofia della scienza ma la non perfetta conoscenza della coordinata esatta del punto ci permette di spostarli, uno ad uno, per farli rientrare in una ipotetica retta che li congiunga.

  Scegliamo il seguente caso:

1. errori omoscedastici per tutti e due gli assi;
2. distribuzione gaussiana per gli errori di ogni punto sui due assi;
3. errori concentrati solo sulle misure, sulla variabile dipendente, cioe' sull'asse Y (la X e' nota senza errore, con Materiali di Riferimento [reference materials], con soluzioni certificate? ecc. {oppure esemplificando un caso reale, l'errore su di essa e', in %, 100 volte piu' piccolo della Y});
4. la media degli errori e' 0 e la distribuzione ha skew=0 (assenza di asimmetria);
5. la retta che meglio descrive l'insieme di punti passa per le coordinate del baricentro della distribuzione, disegnata sul piano euclideo;
6. esiste un numero di misurazioni sufficiente per giustificare la trattazione statistica (media, scarto quadratico, varianza, ecc.).

  Con queste premesse, necessarie per poter usare il metodo O.L.S., iniziamo a disegnare i grafici gia' visti in precedenza.

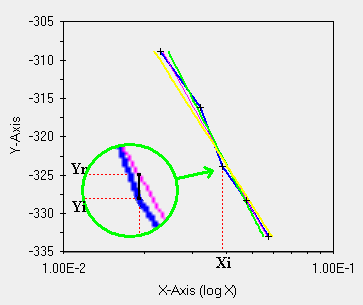
  Dato un valore di Xi, definiamo come Yi il valore misurato e come Yr il valore che si avrebbe (nelle formule Ŷ) su una ipotetica curva di regressione. Si possono avere tante curve di regressione, la gialla, la verde, la viola del grafico qui sopra. Una di queste curve minimizza la distanza fra Yi ed Yr per tutti i valori di Y.

  Conosciamo gia' la formula per trovare la media aritmetica di un set di misure. Anche se abbiamo visto nelle slide dei balestrieri che ci sono altri mezzi per trovare il centroide [centre of location] di una distribuzione, il baricentro si trova con la media aritmetica sulle singole coordinate.

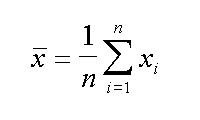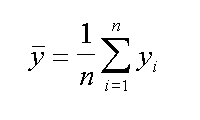la formula della media sulle x	e anche della media sulle y

  Il valore Yi-Yr puo' essere negativo o positivo, prendiamo percio' il valore (Yi - Yr)² e minimizziamo questo valore. Ed ecco in italiano il metodo dei minimi quadrati.

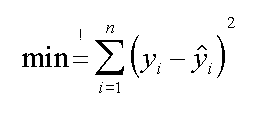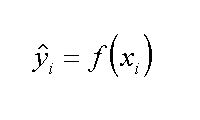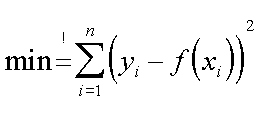minimizziamo la somma dei quadrati	ma la Ŷ e' calcolata dalla f(x)	ecco cosa dobbiamo minimizzare

  Ora bisogna trovare un metodo matematico per calcolare la funzione f(x) e dato che si tratta di una retta (almeno in questa prima ipotesi) i valori dei suoi parametri (pendenza, termine noto, errore residuo, ecc.).

  Tanti, pieni di formule, alcune davvero importanti, alcune ben scritte, altre incomprensibili. Nelle prossime slide qualche riferimento a libri e pagine web. Come sempre per primo il riferimento alla IUPAC.