Rome University, La Sapienza
Chemistry Department
Rome, Italy, Europe		 Dr. Giovanni Visco
Cenni di statistica di base. Calcoli di regressioni e correlazioni. novembre 2005		 Corso di Laurea in
Scienze Applicate ai Beni Culturali ed alla Diagnostica per la loro Conservazione
previous slide, 17b next slide, 19

Ma ora che ci facciamo con la regressione? valori di X regrediti ed errore associato
[but now what we do with the regression? predicted x values and associated errors]

  Fino ad ora tutto il lavoro e' stato concentrato sul definire i punti (sull'asse X) misurare la risposta del sensore-strumento-metodo-ecc., tabellare e graficare il risultato, trovare una zona di linearita', ripetere la misura piu' volte, escludere qualche punto anomalo, ottenere al fine un'equazione della retta.

  Nella ricerca chimico-fisica la regressione e' normalmente utilizzata per ottenere un valore (misurandolo) sull'asse Y e ricavare dall'equazione di regressione un valore sull'asse X. Valore a cui va poi associato un errore di misura.

repetita iuvant

  Diamo alcune regole per ottenere valori regrediti validi:

  1. avere almeno un'idea del valore da misurare*;
  2. preparare una concentrazione a titolo noto simile a quella da misurare;
  3. preparare una soluzione con concentrazione meta' ed una intermedia;
  4. preparare una soluzione con concentrazione doppia ed una intermedia. Si dispone ora di 5 concentrazioni;
  5. misurare i valori di Y associati a queste 5 concentrazioni, partendo dalla concentrazione piu' bassa. Poi misurare il campione incognito;
  6. ripetere il punto precedente per tre volte, consecutivamente. Calcolare le tre equazioni di regressione, con tutti gli errori associati;
  7. scegliere i valori mediani di intercetta e pendenza (a et b);
  8. della curva scelta, mediana, confrontare gli errori associati delle altre due per escludere gravi anomalie nei tre set di misura;
  9. se tutto e' riconducibile all'errore sperimentale trovare il valore mediano delle tre misure incognite.

  Con la procedura precedente abbiamo ristretto di molto l'intervallo di linearita' intorno al valore incognito. Addirittura con un simile metodo si potrebbe utilizzare la regressione lineare anche su metodi-strumenti-sensori non lineari poiche' in un piccolo intervallo qualsiasi curva si puo' approssimare ad una retta accettando qualche errore sui risultati (se si prende una corda di 2 gradi su un cerchio si puo' anche approssimare ad una retta accettando un piccolo errore).

hippo-c
I esempio, elettrodo sensibile allo ione Cl-

  Riprendiamo il caso dell'elettrodo sensibile allo ione Cloro in soluzione acquosa, abbiamo deciso di considerarlo lineare con concentrazioni fra 2.24*10-4 mol/L e 0.1 mol/L (con l'aiuto dei 20 punti usati per la regressione).

  Supponiamo che la nostra soluzione di ioni Cloro abbia una concentrazione intorno a 9.5*10-4 mol/L, simile forse a quella ottenibile dal dilavamento di una parete con efflorescenze.

  Prepariamo percio' una serie di 5 (nel nostro caso 7) concentrazioni di ione Cl- cercando di seguire le indicazioni dei punti precedenti, misuriamo la risposta dell'elettrodo, in mV, in queste concentrazioni, ripetiamo le prove (e/o ripetiamo la preparazione delle concentrazioni), otteniamo come curva mediana la seguente:

Conc. ipotesi C / 3 C / 2 C / 1.5 C=9.5 x 10-4 C * 1.5 C * 2 C * 3
Conc. mol/L 3.10 x 10-4 4.80 x 10-4 7.20 x 10-4 9.50 x 10-4 1.44 x 10-3 1.90 x 10-3 2.80 x 10-3
mV misurati -196.3 -207.3 -217.7 -225.1 -235.6 -242.5 -252.5

  Da cui si ottiene la retta di regressione qui sotto mostrata.

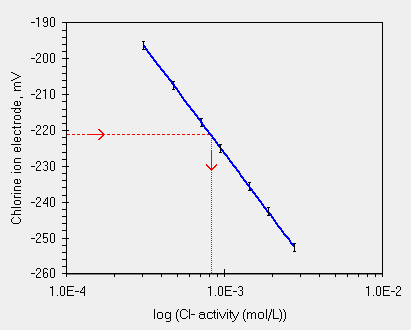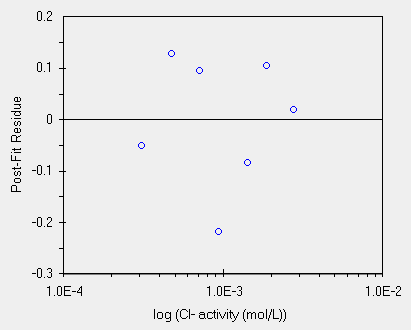una regressione ed i residui
intercetta = -402.8 ± 0.5, pendenza = -58.9 ± 0.17, r = 0.999 ed ecco il grafico dei residui, una buona distribuzione

  Ora che l'elettrodo e' ben conosciuto nelle sue caratteristiche eseguiamo un piccolo numero di misure, ripetute, della soluzione incognita ottenendo i valori qui sotto riportati. Dopo la misura sarebbe buona norma (specie per un elettrodo!) ripetere la retta di regressione e controllare che i parametri siano nei limiti previsti, per controllare che l'elettrodo non sia stato danneggiato dalla matrice incognita.

Prova n. mV misurati Conc. stimata Errore stimato
1 -221.1 8.20 x 10-4 0.02
2 -221.7 8.40 x 10-4 0.02
3 -220.8 8.10 x 10-4 0.02

  Ora abbiamo trovato la concentrazione di ione Cl- della soluzione incognita e cosa piu' importante abbiamo verificato il funzionamento di un metodo che ci potra' essere utile in futuro.

hippo-r
II esempio, analisi mediante spettrofotomeria della concentrazione di un colorante

  La metodologia di indagine e' la stessa, si ipotizza una concentrazione di colorante, si prepara una retta di regressione con almeno 5 punti "intorno" al valore atteso, si misura il valore di assorbanza con lo spettrofotometro (piu' misure) e si ottiene dalla retta di regressione il valore (i valori) della concentrazione.

  Pero', essendo diverso lo strumento sono diversi i passaggi e la manualita' necessaria, se ne parlera' a lezione essendo questa una delle esercitazioni previste in laboratorio.

hippo-l

* ove non si sappia nulla di questo valore, disegnare una retta di regressione estesa dal L.O.D. fino alla saturazione del metodo, senza troppa accuratezza, calcolare una equazione approssimata, misurare il valore incognito (asse Y), dall'equazione approssimata ottenere una stima di X.

previous slide next slide